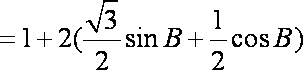- 三角函数中的恒等变换应用
- 共286题
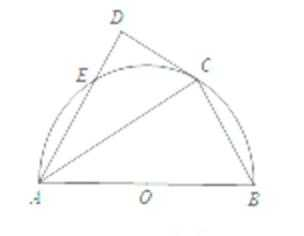
在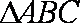

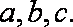
(1)求角A的大小;(2)若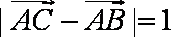
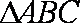
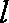
正确答案
(1)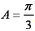
解析
解析:(1)在△ABC中,∵
由正弦定理有: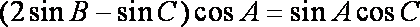
∴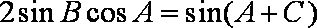
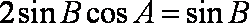
∵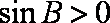
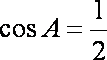
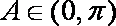

(2)由已知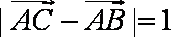
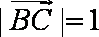
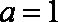
由正弦定理得: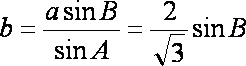
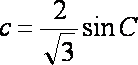
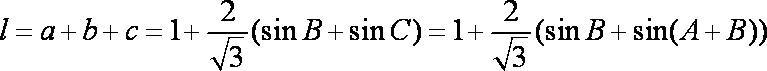
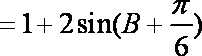
∵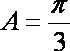
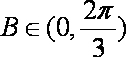
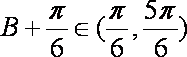
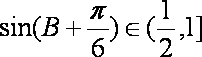
故△ABC的周长l的取值范围是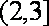
解法二:周长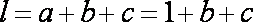
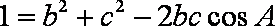
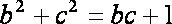
∴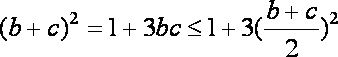
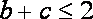
又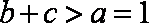
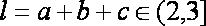
即△ABC的周长l的取值范围是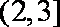
知识点
在
(1)求角A的大小;
(2)若


正确答案
见解析。
解析
(1)∵
∴
即

∴
又

(2)
∴
又由余弦定理得
∴

知识点
已知函数

(1)求函数
(2)若

正确答案
(1)

(2)
解析
(1)由题设
由

故函数


(2)由

考察函数

于是
故

知识点
已知锐角






正确答案
见解析
解析

又






知识点
若sin2x、sinx分别是sinθ与cosθ的等差中项和等比中项,则cos2x的值为
正确答案
解析
依题意有

由①2-②×2得,

又由


知识点
已知

(1)若

(2)若函数y=f(x)的定义域为[
正确答案
(1)
解析
(1)f(x)=-2asin2x+2asinxcosx+a+b=2asin+b,
∵a>0,∴由2kπ-≤2x+≤2kπ+得, kπ-≤x≤kπ+,k∈Z。
∴函数y=f(x)的单调递增区间是[kπ-,kπ+](k∈Z)
(2)x∈[,π]时,2x+∈[,], sin∈[-1,]
当a>0时,f(x)∈[-2a+b,a+b]
当a<0时,f(x)∈[a+b,-2a+b]
综上知,
知识点
已知椭圆



(1) 求椭圆的方程;
(2) 设垂直于



(3) 过点




正确答案
见解析
解析
解:(1)由


(2)设

又

当且仅当
从而

(3)因为A(-1,0),所以
由


∴点
同理,有

∴

即
所以

知识点
已知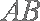

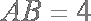


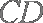
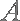
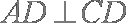

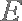
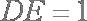
(1)求证: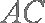
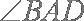
(2)求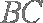
正确答案
见解析
解析
(1)连结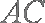
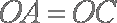
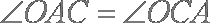
因为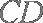
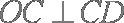
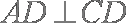
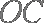
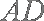
所以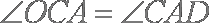
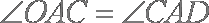
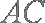
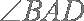
(2)由(1)知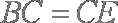
连结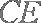
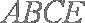

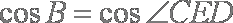
所以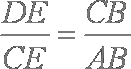
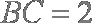
知识点
设函数



(1)求
(2)在








正确答案
见解析
解析
(1)

令

(2)由


∵
又∵

∴在

由

知识点
设函数



(1)求
(2)在








正确答案
见解析
解析
(1)

令

(2)由


∵
又∵

∴在

由

知识点
扫码查看完整答案与解析