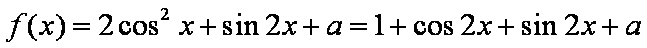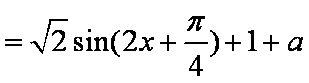- 三角函数中的恒等变换应用
- 共286题
设函数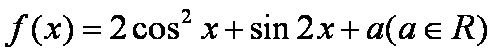
(1)求函数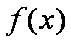
(2)当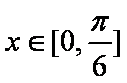
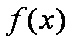
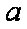
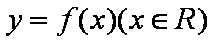
正确答案
见解析
解析
解:(1)
则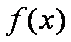
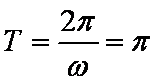
且当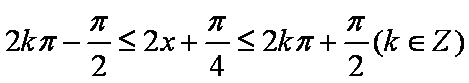
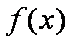
即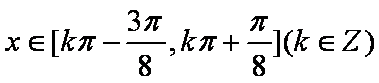
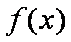
(2)当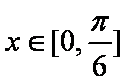
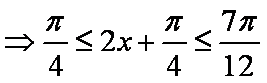
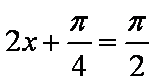
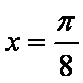
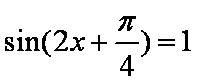
所以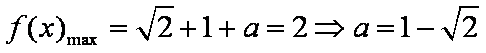
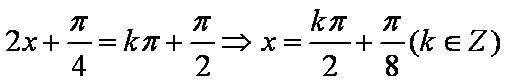
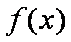
知识点
已知向量




(1)求
(2)当


正确答案
见解析。
解析
(1) 




∵θ∈[π,2π],∴



(2) 由已知

又

∵θ∈[π,2π]∴
知识点
15.若函数


正确答案
(-1,0)∪(1,+∞)
解析
解析已在路上飞奔,马上就到!
知识点
15.在△ABC中,a,b,c分别为内角A,B,C的对边,且b2+c2-a2=bc.
(1)求角A的大小;
(2)设函数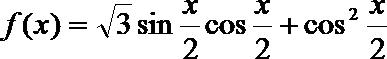
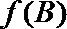
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.在




(1)求角
(2)若

正确答案
(1)由已知等式得:
(2)
解析
解析已在路上飞奔,马上就到!
知识点
21.已知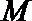
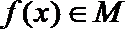
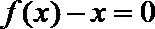
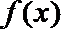
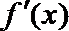
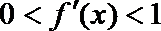
(Ⅰ)集合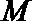
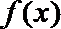
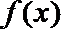
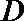
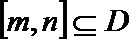
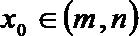
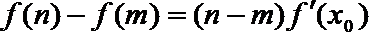
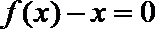
(Ⅱ)对任意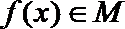
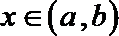
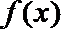
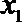
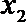
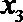
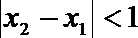
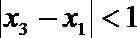
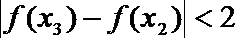
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知图①中的图象对应的函数为y=f(x),则图②的图象对应的函数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知函数①

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析