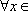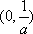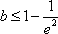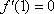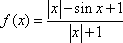- 函数概念与表示
- 共2805题
已知函数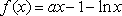
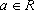
(1)讨论函数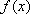
(2)若函数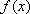
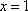
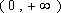
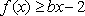
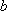
正确答案
(1)当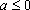
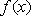
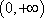
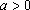
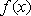
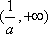
(2)
解析
(1)在区间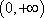
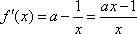
①若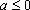
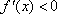
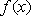
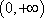
②若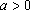
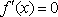
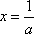
在区间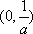
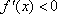
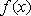
在区间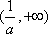
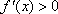
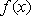
综上所述,①当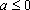
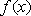
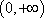
②当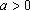
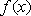
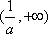
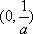
(2)因为函数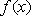
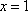
解得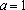
由已知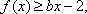
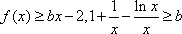
令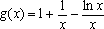
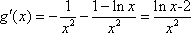
易得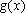
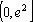
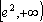
所以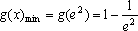
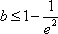
知识点
已知函数

(1)若曲线
(2)当

正确答案
见解析
解析
(1)函数h(x)定义域为{x|x≠-a},…………………………………………………1分
则





(2)记






令















单调递减区间为



① 当




② 当






③当




综上所述,当





知识点
已知函
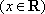
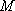
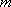
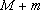
正确答案
2
解析
略
知识点
已知函数


正确答案
解析
略
知识点
设函数
正确答案
解析
A显然正确;
∵
∵D(x+1)=
∵D(

知识点
已知f是有序数对集合




则

正确答案
8;
解析
略
知识点
已知函数

(1)试讨论

(2)当







正确答案
见解析
解析
(1)解:由已知

由


因为


所以在区间



故


(2)证明:由题意可得,当



即 
所以

因为


所以

所以

令



所以


所以
知识点
在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,如果函数



① 



其中是一阶整点函数的是( )
正确答案
解析
略
知识点
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=2AA1,∠BAC=120°,D,D1分别是线段BC,B1C1的中点,P是线段AD的中点。
(1)在平面ABC内,试作出过点P与平面A1BC平行的直线l,说明理由,并证明直线l⊥平面ADD1A1;
(2)设(1)中的直线l交AB于点M,交AC于点N,求二面角A-A1M-N的余弦值。
正确答案
见解析
解析
(1)如图,在平面ABC内,过点P作直线l∥BC,
因为l在平面A1BC外,BC在平面A1BC内,由直线与平面平行的判定定理可知,l∥平面A1BC。
由已知,AB=AC,D是BC的中点,
所以,BC⊥AD,则直线l⊥AD。
因为AA1⊥平面ABC,
所以AA1⊥直线l.
又因为AD,AA1在平面ADD1A1内,且AD与AA1相交,
所以直线l⊥平面ADD1A1.
(2)解法一:
连接A1P,过A作AE⊥A1P于E,过E作EF⊥A1M于F,连接AF.
由(1)知,MN⊥平面AEA1,
所以平面AEA1⊥平面A1MN.
所以AE⊥平面A1MN,则A1M⊥AE.
所以A1M⊥平面AEF,则A1M⊥AF.
故∠AFE为二面角A-A1M-N的平面角(设为θ)。
设AA1=1,则由AB=AC=2AA1,∠BAC=120°,有∠BAD=60°,AB=2,AD=1.
又P为AD的中点,
所以M为AB中点,且AP=
所以,在Rt△AA1P中,A1P=

从而

所以sin θ=
所以cos θ=
故二面角A-A1M-N的余弦值为
解法二:设A1A=1.如图,过A1作A1E平行于B1C1,以A1为坐标原点,分别以


则A1(0,0,0),A(0,0,1)。
因为P为AD的中点,
所以M,N分别为AB,AC的中点。
故M

所以




设平面AA1M的一个法向量为n1=(x1,y1,z1),
则
故有
从而
取x1=1,则y1=
所以n1=(1,
设平面A1MN的一个法向量为n2=(x2,y2,z2),
则
故有
从而
取y2=2,则z2=-1,所以n2=(0,2,-1)。
设二面角A-A1M-N的平面角为θ,
又θ为锐角,
则cos θ=
=
故二面角A-A1M-N的余弦值为
知识点

正确答案
3
解析
略
知识点
扫码查看完整答案与解析