- 函数概念与表示
- 共2805题
已知函数
(1)当a=1时,∃x0∈[1,e]使不等式f(x0)≤m,求实数m的取值范围;
(2)若在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax的下方,求实数a的取值范围
正确答案
见解析。
解析
(1)当a=1时,
可知当x∈[1,e]时f(x)为增函数,
最小值为
要使∃x0∈[1,e]使不等式f(x0)≤m,即f(x)的最小值小于等于m,
故实数m的取值范围是
(2)已知函数
若在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax的下方,
等价于对任意x∈(1,+∞),f(x)<2ax,
即
设
即g(x)的最大值小于0.
(1)当

∴
∴g(1)=﹣a﹣
∴a≥﹣
∴
(2)a≥1时,

g(x)无最大值,即最大值可无穷大,故此时不满足条件。
(3)当


同样最大值可无穷大,不满足题意,综上,实数a的取值范围是
知识点
已知函数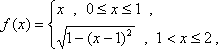


正确答案
解析
略
知识点
已知函数


(1)若


(2)求
正确答案
(1)
(2) 当







解析

(1)因为

所以


经检验,当




(2)


(1)当


此时

所以当





(2)当


即


所以当


知识点
已知函数

正确答案
解析
略
知识点
已知函数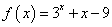
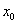
正确答案
解析
∵函数f(x)=3x+x﹣9在R上连续,f(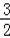
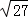
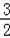
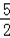
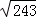
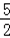
f(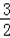
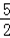
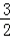
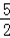
故选D
知识点
设M是由满足下列条件的函数




(1)判断函数
(2)集合M中的元素





(3)设






正确答案
见解析。
解析
(1)因为
所以

又因为当



所以函数
(2)假设方程

则
不妨设
使得等式
因为


所以方程
(3)不妨设



又因为

所以
所以

所以
知识点
设某商品的需求函数为






正确答案
解析
略
知识点
一张正方形的纸片,剪去两个一样的小矩形得到一个“






正确答案
解析
由题意,得

知识点
若复数

正确答案
1
解析
略
知识点

正确答案
2
解析
∵∫0π(sinx+cosx)dx
=(﹣cosx+sinx)|0π=(﹣cosπ+sinπ)﹣(﹣cos0+sin0)
=2。
故答案为:2。
知识点
扫码查看完整答案与解析