- 函数概念与表示
- 共2805题
函数y=ln|x﹣1|的图象与函数y=﹣2cosπx(﹣2≤x≤4)的图象所有交点的横坐标之和等于( )
正确答案
解析
由图象变化的法则可知:
y=lnx的图象作关于y轴的对称后和原来的一起构成y=ln|x|的图象,向右平移1个单位得到y=ln|x﹣1|的图象,再把x轴上方的不动,下方的对折上去可得g(x)=ln|x﹣1||的图象;
又f(x)=﹣2cosπx的周期为T=2,如图所示:
两图象都关于直线x=1对称,且共有6个交点,
由中点坐标公式可得:xA+xB=﹣2,xD+xC=2,xE+xF=6
故所有交点的横坐标之和为6
故选B
知识点
已知函数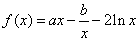
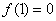
(1)若函数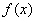
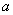
(2)若函数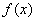
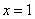
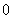
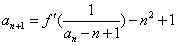
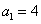
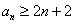
(3)在(2)的条件下,试比较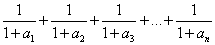
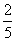
正确答案
见解析。
解析
(1)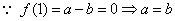
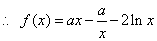
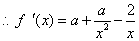
要使函数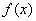
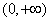
① 当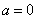
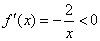
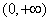
此时函数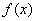
②当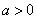
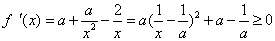
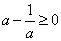
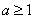
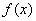
③ 当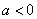
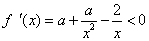
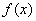
综上所述,实数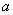
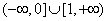
(2)由题意知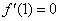
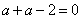
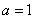
于是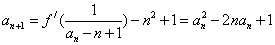
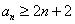
(i)当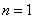
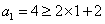
(ii)假设当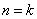
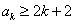
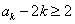
则当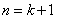
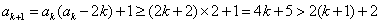
所以当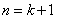
由(i)(ii)知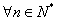
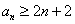
(3) 由(2)得
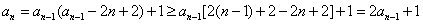
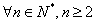
于是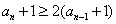
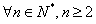
所以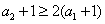
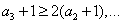
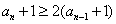
累乘可得: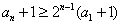
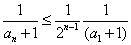
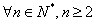
所以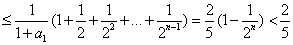
知识点
下列四个函数中,既是定义域上的奇函数又在区间
正确答案
解析
略
知识点
定义函数y=f(x),x∈D,若存在常数C,对任意的x1∈D,存在唯一的x2∈D,使得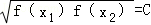
正确答案
解析
根据已知中关于函数f(x)在D上的几何平均数为C的定义,
结合f(x)=2x在区间[1,2]单调递增
则x1=1时,存在唯一的x2=2与之对应
故C=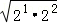
故选C。
知识点
集合A={x|2012<x<2013},B={x|x>a}可满足A∩B=ϕ,则实数a的取值范围( )
正确答案
解析
解:将集合A={x|2012<x<2013},B={x|x>a}画在数轴上
根据A∩B=∅,
∴a≥2013。
故选C
知识点
已知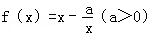
(1)若对[1,+∞)内的一切实数x,不等式f(x)≥g(x)恒成立,求实数a的取值范围;
(2)当a=1时,求最大的正整数k,使得对[e,3](e=2.71828…是自然对数的底数)内的任意k个实数x1,x2,…,xk都有f(x1)+f(x2)+…+f(xk﹣1)≤16g(xk)成立;
(3)求证: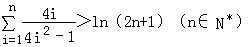
正确答案
见解析。
解析
(1)设点(x0,y0)为直线y=2x﹣2与曲线y=g(x)的切点,则有2lnx0+bx0=2x0﹣2①
∵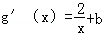
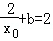
由②得,2x0﹣2=bx0,代入①得x0=1,所以b=0,则g(x)=2lnx。
由f(x)≥g(x),即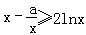
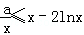
∵x≥1,∴要使不等式f(x)≥g(x)恒成立,必须a≤x2﹣2xlnx恒成立。
设h(x)=x2﹣2xlnx,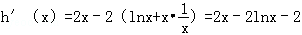
∵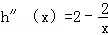
∴h'(x)≥h'(1)=0,∴h(x)是增函数,则h(x)≥h(1)=1,∴a≤1。
又a>0,因此,实数a的取值范围是0<a≤1.
(2)当a=1时,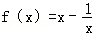
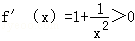
f(x)在[e,3]上的最大值为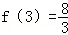
要对[e,3]内的任意k个实数x1,x2,…,xk,都有f(x1)+f(x2)+…+f(xk﹣1)≤16g(xk)成立,
必须使得不等式左边的最大值小于或等于右边的最小值,∵当x1=x2=…=xk﹣1=3时不等式左边取得最大值,
xk=e时不等式右边取得最小值,∴(k﹣1)f(3)≤16g(3),即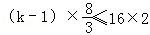
因此,k的最大值为13.
(3)证明:1°当n=1时,左边=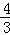
根据(1)的推导有,x∈(1,+∞)时,f(x)>g(x),即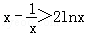
令x=3,得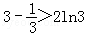
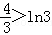
因此,n=1时不等式成立,
2°假设当n=k时不等式成立,即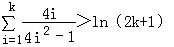
则当n=k+1时,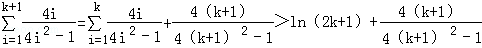
要证n=k+1时命题成立,即证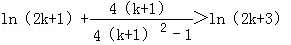
即证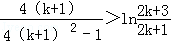
在不等式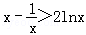
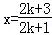
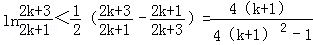
∴n=k+1时命题也成立,
综上所述,不等式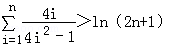
知识点
已知变量x,y满足约束条件
正确答案
[﹣
解析
解:∵变量x,y满足约束条件
目标函数为:z=3x﹣y,
直线4x﹣y+1=0与x+2y﹣2=0交于点A(0,1),
直线2x+y﹣4=0与x+2y﹣2=0交于点B(2,0),
直线4x﹣y+1=0与2x+y﹣4=0交于点C(
可知z在点C处取得最小值,zmin=3×

z在点B处取得最大值,zmax=3×2﹣0=6,
∴﹣
故答案为[﹣
知识点
已知函数
(1)求点A、B的坐标以及
(2)设点A、B分别在角α、β的终边上,求tan(α﹣2β)的值。
正确答案
见解析。
解析
解:(1)∵ 0≤x≤5,∴
∴ 
当

f(x)取得最大值2;
当

因此,点A、B的坐标分别是A(1,2)、B(5,﹣1),
∴
(2)∵点A(1,2)、B(5,﹣1)分别在角α、β的终边上,
∴tanα=2,
∵
∴
知识点
一次考试中,五名同学的数学、物理成绩如下表所示:
(1)请在如图的直角坐标系中作出这些数据的散点图,并求出这些数据的回归方程;
(2)要从4名数学成绩在90分以上的同学中选2人参加一项活动,以X表示选中的同学的物理成绩高于90分的人数,求随机变量X的分布列及数学期望E(X)的值。
正确答案
见解析。
解析
(1)散点图如图所示,

=93,

=90,
知识点
函数f(x)的定义域为D,若对任意的x1、x2∈D,当x1<x2时,都有f(x1)≤f(x2),则称函数f(x)在D上为“非减函数”,设函数g(x)在[0,1]上为“非减函数”,且满足以下三个条件:
(1)g(0)=0;
(2)
(3)g(1﹣x)=1﹣g(x),
则g(1)= ;
正确答案
1;
解析
①在(3)中令x=0得g(1)=1﹣g(0)=1,∴g(1)=1;
②在(2)中令x=1得



∵


故答案分别为1,
知识点
扫码查看完整答案与解析