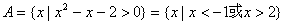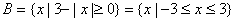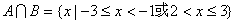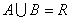函数概念与表示
共2805题

函数概念与表示
共2805题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

已知两条不同的直线m，n和两个不同的平面，，以下四个命题：

①若m//，n//，且//，则m//n ②若m//，n⊥，且⊥，则m//n

③若m⊥，n//，且//，则m⊥n ④若m⊥，n⊥，且⊥，则m⊥n

A1个

B2个

C3个

D4个

正确答案

解析

略

知识点

函数的概念及其构成要素

题型：简答题

简答题 · 13 分

已知函数。

（1）当时，求函数的单调递减区间；

（2）求函数的极值；

（3）若函数在区间上恰有两个零点，求的取值范围。

正确答案

见解析

解析

（1）依题意，函数的定义域为，

当时，，

……………………2分

由得，即

解得或，

又，

的单调递减区间为。 ……………………4分

（2），

1）时，恒成立

在上单调递增，无极值. ……………………6分

2）时，由于

所以在上单调递增，在上单调递减，

从而。 ……………………9分

（3）由（2）问显然可知，

当时，在区间上为增函数，

在区间不可能恰有两个零点。 ……………………10分

当时，由（2）问知，

又，为的一个零点。 ……………………11分

若在恰有两个零点，只需

即 ……………………13分

知识点

函数的概念及其构成要素

题型：简答题

简答题 · 14 分

已知是函数的反函数，

（1）解关于的不等式：；

（2）当时，过点是否存在函数图象的切线？若存在，有多少条？若不存在，说明理由；

（3）若是使恒成立的最小值，试比较与的大小。

正确答案

见解析。

解析

（1）由已知可得，当时，的定义域为；当时，

的定义域为

①当时，，原不等式等价于：，

可得；

②当时，，原不等式等价于：，

可得。 4分

（2）设图象上的切点坐标为，显然，

可得，

，可得，

所以没有实根，故不存在切线。，9分

（3）对恒成立，所以，

令，可得在区间上单调递减，

故，，得，。

令，，而，即

，所以，

=。 14分

知识点

函数的概念及其构成要素

题型：简答题

简答题 · 12 分

记函数的定义域为集合A，函数的定义域为集合B。

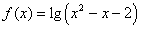
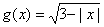
（1）求A∩B和A∪B；

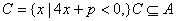
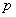
（2）若，求实数的取值范围。

正确答案

见解析。

解析

（1）依题意，得

∴

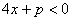
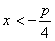
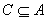
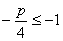
（2）由，得，而，∴，∴

知识点

函数的概念及其构成要素

题型：单选题

单选题 · 5 分

已知下列命题：①；②命题p：，则；③“”是“”的充分不必要条件；④已知随机变量，其中真命题有

A1个

B2个

C3个

D4个

正确答案

解析

略

知识点

函数的概念及其构成要素

题型：填空题

填空题 · 4 分

设为常数，函数，若在上是增函数，则的取值范围是___________.

正确答案

解析

略

知识点

函数的概念及其构成要素

题型：填空题

填空题 · 5 分

已知点P（x，y）满足，则点Q（x+y，y）构成的图形的面积为　　。

正确答案

解析

令x+y=u，y=v，则点Q（u，v）满足，

在平面内画出点Q（u，v）所构成的平面区域如图，

它是一个平行四边形，一边长为1，高为2，

故其面积为2×1=2。

故答案为：2。

知识点

函数的概念及其构成要素

题型：简答题

简答题 · 14 分

设，函数的图像与函数的图像关于点对称。

（1）求函数的解析式；

（2）若关于的方程有两个不同的正数解，求实数的取值范围。

正确答案

（1）（2）

解析

（1）设点是函数图像上任意一点，关于点对称的点为，则，，于是，，………………2分

因为在函数的图像上，所以，…4分

即，，

所以。……………………………………………………6分

（2）令，因为，，所以，

所以方程可化为，…………………………………………8分

即关于的方程有大于的相异两实数解。

作，则，………………………………………12分

解得；所以的取值范围是。

知识点

函数的概念及其构成要素

题型：填空题

填空题 · 4 分

已知，若存在区间，使得，则实数的取值范围是___________.

正确答案

解析

略

知识点

函数的概念及其构成要素

题型：单选题

单选题 · 5 分

如果函数的图像与曲线恰好有两个不同的公共点，则实数的取值范围是

正确答案

解析

略

知识点

函数的概念及其构成要素

继续学习学习下一知识点

下一知识点 : 函数的基本性质

百度题库 > 高考 > 理科数学 > 函数概念与表示

扫码查看完整答案与解析