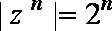- 函数概念与表示
- 共2805题
已知函数f(x)=
(1)求函数f(x)的单调递增区间;
(2)设△ABC的内角A,B,C所对的边分别是a,b,C.若f(A)=2,a=
正确答案
见解析。
解析
(1)由三角函数中的恒等变换应用化简解析式可得f(x)=2sin(ωx﹣



(2)由f(A)=2,可得sin(2A﹣




(1)∵f(x)=
∴f(x)=2sin(ωx﹣
∴函数f(x)的最大值为2.
∵函数f(x)的图象与直线y=2的相邻两个交点之间的距离为π,
∴T=π,
∴
∴f(x)=2sin(2x﹣
令2k


解得k

∴函数f(x)的单调递增区间是[k

(2)由(1)知,f(x)=2sin(2x﹣
在△ABC中,∵f(A)=2,
∴2sin(2A﹣
∴sin(2A﹣
∵0<A<π,
∴A=
∵a=

∴sin

∴sinB=
∵a>b,
∴A>B,
∴0
∴B=
知识点
设函数
(1)求
(2)当



(3)证明:当

正确答案
见解析
解析
(1)
①



②当


∴


(2)当



又
∴
∴当

(3)∵

只需证:
设
则
由(1)知

∴


∴
知识点
7.已知


正确答案
解析
因为









知识点
设命题p:函数




正确答案
解析




对于x


q真
p

实数对(a,b)为坐标的点的轨迹图形如图(阴影部分, 不包括边界。)
解:


S=



=(



知识点
若函数f(x)满足:∀x1,x2∈[﹣1,1],都有|f(x1)﹣f(x2)|≤|x1﹣x2|成立,则称f(x)∈Ψ,对于函数g(x)=x3﹣x,h(x)=
正确答案
解析
|g(x1)﹣g(x2)|=|x13﹣x1﹣x23+x2|=|(x1﹣x2)•(x12+x1x2+x22)﹣(x1﹣x2)|=|(x1﹣x2)||x12+x1x2+x22﹣1|,
因为x1,x2∈[﹣1,1],
所以|x12+x1x2+x22|≤x12+|x1x2|+x22≤3
所以|x12+x1x2+x22﹣1|≤|x12+x1x2+x22﹣1|≤|x12+|x1x2|+x22﹣1|≤|3﹣1|≤2
所以有|g(x1)﹣g(x2)|≤2|x1﹣x2|,
所以g(x)∉Ψ;
当﹣1≤x<0时,|h(x1)﹣h(x2)|=|x1﹣x2|≤|x1﹣x2|,
当0≤x≤1时,|h(x1)﹣h(x2)|=|cosx1﹣cosx2|≤|x1﹣x2|,
所述h(x)∈Ψ,
故选:C.
知识点
已知函数f(x)=ax﹣a•x,a≥e,e=2.71828…为自然对数的底数。
(1)当a=e时,求函数f(x)在点(1,f(1))处的切线方程;
(2)设n∈N*,比较
正确答案
见解析。
解析
(1)当a=e时,求导数,确定切线的斜率,即可求函数f(x)在点(1,f(1))处的切线方程;
(2)
(1)∵a=e时,f(x)=ex﹣ex,
∴f′(x)=ex﹣e,
∴f′(1)=0,f(1)=0,
于是f(x)在点(1,f(1))处的切线方程为y=0。
(2)
理由如下:因为a≥e,
欲证
只需证
只需证an>na﹣1。
构造函数

因为a≥e,所以lna≥1。
令g′(x)>0,得x<

所以函数g(x)在(﹣∞,

所以函数g(x)的最大值为


所以

ax﹣ax+1=a[ax﹣1﹣(x﹣1)]+1﹣a≥a[e(x﹣1)lna﹣(x﹣1)]+1﹣a
>a[2(x﹣1)﹣(x﹣1)]+1﹣a=a(x﹣2)+1>0,
所以ax>ax﹣1。
取x=n,得an>na﹣1成立,
所以当a≥e时,
知识点
14.观察下列等式:
(1)若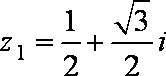


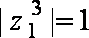

(2)若
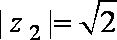

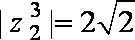

依据你发现的规律,若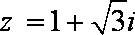

正确答案
解析
由(1)可知模长为1的复数的任何次方的模还是1,由(2)可知任何复数都可以化为一个非负实数乘以一个对应的模长为1的复数,结合(1)(2),
可知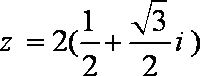
知识点
函数


(1)若

(2)若


正确答案
(1)[3,
(2)
解析
(1)由已知得:
又




因为

函数

(2)因为

由x0
所以,
故

知识点
已知

(1)求
(2)若


(3)证明:

正确答案
见解析
解析
(1)函数


当


(2)



又



(3)由 (2),取

则



所以
知识点
已知





(
(1)求函数
(2)设∆ABC的内角A,B,C的对边分别为a,b,c且


正确答案
见解析
解析
解.(1) 
则

最小正周期是
(2)








由余弦定理,得

由解得
知识点
扫码查看完整答案与解析