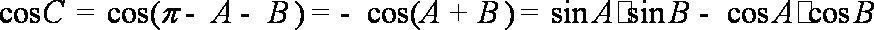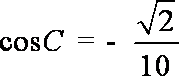- 函数概念与表示
- 共2805题
15.已知A、B、C是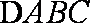
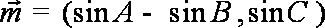
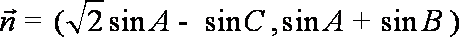
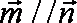
(1)求角B的大小;
(2)若
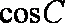
正确答案
见解析。
解析
(1)∵向量
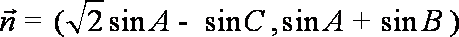
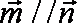
所以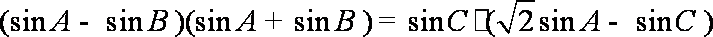
由正弦定理可得:
再由余弦定理可得: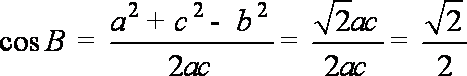
(2)由(1)得
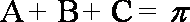
所以

所以
知识点
5.设


正确答案
解析

令




知识点
12.已知函数




正确答案
解析
如图是函数






知识点
4.已知函数

正确答案
解析



知识点
19.设函数
(1)若曲线


(2)讨论
(3)讨论方程
正确答案
见解析。
解析
(1)因为曲线




所以
(2)因为
所以当




当






在
(3)因为方程

令


解得x=-1(舍),x=1,所以

所以
当b-1>0即b>1时,方程
当b=1时,方程
当b<0时,方程
知识点
7.已知


正确答案
解析
因为









知识点
8.设函数



正确答案
解析
因为函数







知识点
21.已知

(1)

(2)记


(3)是否存在


正确答案
见解析。
解析
(1)
(2)当0≤x≤t时,f(x)=

因此,当x∈(0,t)时,f′(x)=
当x∈(t,+∞)时,f′(x)=
①若t≥6,则f(x)在(0,6)上单调递减,g(t)=f(0)=
②若0<t<6,则f(x)在(0,t)上单调递减,在(t,6)上单调递增。
所以g(t)=mtx{f(0),f(6)}。
而f(0)-f(6)=

当2<t<6时,g(t)=f(0)=
(3)由(1)知,当t≥6时,f(x)在(0,6)上单调递减,故不满足要求。
当0<t<6时,f(x)在(0,t)上单调递减,在(t,6)上单调递增。
若存在x1,x2∈(0,6)(x1<x2),使曲线y=f(x)在(x1,f(x1)),(x2,f(x2))两点处的切线互相垂直,则x1∈(0,t),x2∈(t,6),且f′(x1)·f′(x2)=-1,
即

由x1∈(0,t),x2∈(t,6)得x1+3t∈(3t,4t),

故(*)成立等价于集合T={x|3t<x<4t}与集合B=



综上所述,存在t使函数f(x)在区间(0,6)内的图象上存在两点,在该两点处的切线互相垂直,且t的取值范围是
知识点
7.已知函数f(x)=
正确答案
解析
∵函数f(x)=

知识点
16.已知函数

(1)求函数
(2)已知







正确答案
(1)


(2)
解析
(1)

由




(2)∵

∵


即

由余弦定理

即
∴
知识点
扫码查看完整答案与解析