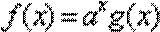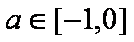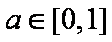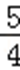- 函数概念与表示
- 共2805题
6.已知函数f(x)=
正确答案
解析
由于f(x)=
且f(x)在区间(﹣∞,+∞)上是增函数,
则当x≥0时,y=x2显然递增;
当x<0时,y=x3+a2﹣3a+2的导数为y′=3x2≥0,则递增;
由f(x)在R上单调递增,
则02≥03+a2﹣3a+2,即为a2﹣3a+2≤0,
解得,1≤a≤2.
故选C.
知识点
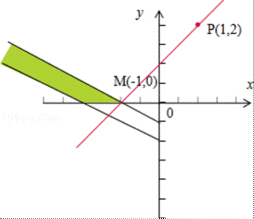
9.已知实数x,y满足约束条件

正确答案
解析
由题意得:作出目标函数2x+y=6,和2x+y=1,
则对应的平面区域如图:则B,C在直线ax+by+c=0上,
由

由

则B,C在直线在直线ax+by+c=0上,∴BC的方程为3x﹣y﹣4=0,
即a=3,b=﹣1,c=﹣4,则
知识点
8.以下有五个结论:
①某校高三一班和高三二班的人数分别是


②若x1,x2,…,x10的平均数为a,方差为b,则x1+5,x2+5,…,x10+5的平均数为a+5,方差为b+25.;
③从总体中抽取的样本



其中正确结论的个数有( )
正确答案
解析
略。
知识点
11.用1,2,3,4,5,6组成数字不重复的六位数,满足1不在左右两端,2,4,6三个偶数中有且只有两个偶数相邻,则这样的六位数的个数为( )
正确答案
解析
从2,4,6三个偶数中任意选出2个看作一个“整体”,方法有

①若1排在左端,方法有





②若1排在右端,同理求得满足条件的六位数也有72种,
③若1排在中间,方法有
根据分步计数原理求得此时满足条件的六位数共有6×

综上,满足条件的六位数共有 72+72+144=288种,
故选B.
知识点
16.已知函数










正确答案
2
解析
由已知得M(0,2a),N(a,0),因为





知识点
8.已知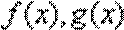
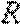
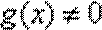
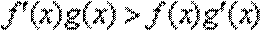
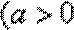

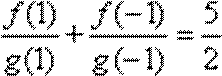
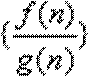
正确答案
解析
∵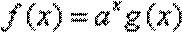
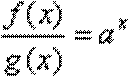
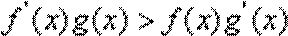
∴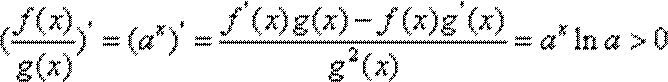
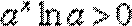
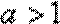
∵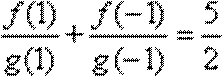
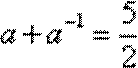
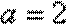
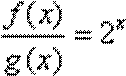
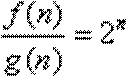
∴数列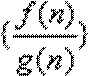
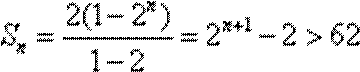
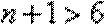
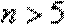
所以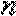
知识点
12.函数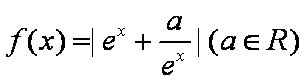
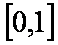
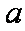
正确答案
解析
当a>0时,y=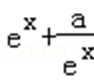
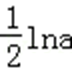
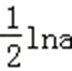
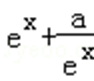
若函数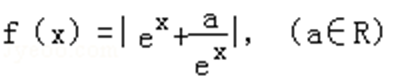
则y=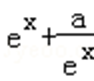
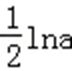
当a=0时,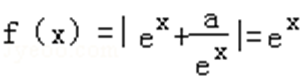
当a<0时,


则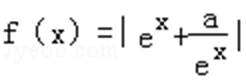


则ln
综上,实数a的取值范围是[﹣1,1],故选C。
知识点
21.已知中心在原点,焦点在


(1)求椭圆C的方程;
(2)是否存在过点




正确答案
(1)
(2) 存在,
解析
(1)设椭圆C的方程为


(2)假设存在直线l1且由题意得斜率存在,设满足条件的方程为y=k1(x-2)+1,
代入椭圆C的方程得,(3+4k)x2-8k1(2k1-1)x+16k-16k1-8=0.因为直线l1与椭圆C相交于不同的两点A,B,
设A,B两点的坐标分别为(x1,y1),(x2,y2),
所以Δ=[-8k1(2k1-1)]2-4(3+4k)·(16k-16k1-8)=32(6k1+3)>0,所以k1>-.又

即(x1-2)(x2-2)+(y1-1)(y2-1)=,所以(x1-2)(x2-2)(1+

即[x1x2-2(x1+x2)+4](1+

所以




知识点
22.已知函数
(1)当


(2)设函数

(3)若在




正确答案
(1)y=1;
(2)




(3)

解析
(1)

当








(2)
①当





所以








(3)在











所以



因为

②当



所以



③当



因为

此时不存在

综上可得所求


知识点
12.定义在R上的可导函数f(x)=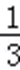
正确答案
解析
∵f(x)=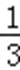
∴f′(x)=x2+ax+2b,
∵函数f(x)在区间(0,1)内取得极大值,在区间(1,2)内取得极小值,
∴f′(x)=x2+ax+2b=0在(0,1)和(1,2)内各有一个根,
f′(0)>0,f′(1)<0,f′(2)>0,
即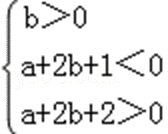
若(1﹣t)a+b+t﹣3>0恒成立,可知a+b﹣3>t(a﹣1)恒成立,由可行域可知a<0,
可得t>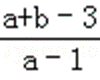
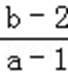
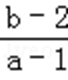
则最小值为1+1=2,
∴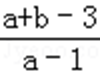
故选:B.
知识点
扫码查看完整答案与解析