热门试卷

（1）。

若，则，时，。此时，在区间上为增函数。

∴  时，。符合要求。

若，则方程有两个异号的实根，设这两个实根为，，且。

∴  时，。在区间上为减函数，。

∴  不符合要求。

∴  的取值范围为。  

（2）由（1）知，时，不等式恒成立。

∴  时，恒成立。

令（），得，

整理得 。

∴  。令，2，3，…，，得

，，，…，。

将上述个不等式的左右两边分别相加，得

。

∴  对一切正整数均成立。

（1）函数 f（x）=x2+4|x﹣a|=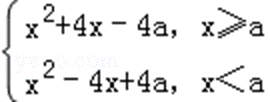，由题意可得函数f（x）在[﹣1，1]上不单调，

当a≥1时，函数f（x）在[﹣1，1]上单调递减，不满足条件.

当a≤时，函数f（x）在[﹣1，1]上单调递增，不满足条件.

∴﹣1＜a＜1，此时，函数f（x）在[﹣1，a]上单调递减，在（a，1]上单调递增，

（2）∵对任意的x1、x2∈[﹣1，1]，都有|f（x1）﹣f（x2）|≤k成立，

设函数f（x）在[﹣1，1]上的最大值为M（a），最小值为m（a），

当a≥1时，函数f（x）在[﹣1，1]上单调递减，M（a）=f（﹣1）=4a+5，m（a）=f（1）=4a﹣3．

当a≤时，函数f（x）在[﹣1，1]上单调递增，M（a）=f（1）=5﹣4a，m（a）=f（﹣1）=﹣4a﹣3．

∴﹣1＜a＜1，函数f（x）在[﹣1，a]上单调递减，在（a，1]上单调递增，m（a）=f（a）=a2，M（a）=max{f（1），f（﹣1）}={5﹣4a，5+4a}．

即当0＜a＜1时，M（a）=5+4a，当﹣1＜a＜0时，M（a）=5﹣4a．

综上可得，M（a）﹣m（a）=，由对任意的x1、x2∈[﹣1，1]，|f（x1）﹣f（x2）|≤k恒成立，

可得k≥M（a）﹣m（a），

故当a≥1 或a≤﹣1时，k≥8；

当0≤a＜1时，k≥﹣a2+4a+5=9﹣（a﹣2）2，由9﹣（a﹣2）2∈[5，8），可得k≥8；

当﹣1＜a≤0时，k≥﹣a2﹣4a+5=9﹣（a+2）2，由9﹣（a+2）2∈[5，8），可得k≥8．

综合可得，k≥8。