函数概念与表示_章节学习

1

题型：简答题

|

简答题 · 14 分

19.设函数，

（1）若曲线在点处的切线方程为，求a，b的值；

（2）讨论的单调性；

（3）讨论方程根的个数。

正确答案

见解析。

解析

（1）因为曲线在点处的切线方程为，而，所以，

所以，即

（2）因为，

所以当，即时，恒成立，此时的单调性在单调递增。

当时，令，可得，，所以在和单调递增，

在单调递减。

（3）因为方程可化为，

令，，令，

解得x＝－1(舍)，x＝1，所以在(0,1)单调递减，在单调递增，

所以，

当b－1＞0即b＞1时，方程无解；

当b＝1时，方程有唯一解；

当b＜0时，方程有两解。

知识点

函数的概念及其构成要素

1

题型：简答题

|

简答题 · 13 分

21.如图，设AB为⊙O的任一条不与直线l垂直的直径，P是⊙O与l的公共点，AC⊥l，BD⊥l，垂足分别为C，D，且PC=PD。

（1）求证：l是⊙O的切线；

（2）若⊙O的半径OA=5，AC=4，求CD的长。

正确答案

见解析。

解析

（1）证明：连接OP，因为AC⊥l，BD⊥l，

所以AC∥BD．

又OA=OB，PC=PD，

所以OP∥BD，从而OP⊥l．

因为P在⊙O上，所以l是⊙O的切线．

（2）

由上知OP=（AC+BD），

所以BD=2OP﹣AC=6，

过点A作AE⊥BD，垂足为E，则BE=BD﹣AC=6﹣4=2，

在Rt△ABE中，AE==4，

∴CD=4．

知识点

函数的概念及其构成要素

1

题型：简答题

|

简答题 · 12 分

21.已知函数

（1）若，判断函数在定义域内的单调性；

（2）若函数在内存在极值，求实数m的取值范围。

正确答案

（1）当单调递增；当单调递减。

（2）

解析

（1）显然函数定义域为（0，+）若m=1，

令

当单调递增；

当单调递减。

（2）

令

当单调递增；

当单调递减。

故当有极大值，根据题意

知识点

函数的概念及其构成要素

1

题型：简答题

|

简答题 · 14 分

20.已知函数.

（1）求函数的单调区间；

（2）若函数上是减函数，求实数a的最小值；

（3）若，使成立，求实数a的取值范围。

正确答案

见解析。

解析

由已知函数的定义域均为,且.

（1）函数,

当且时,;当时,.

所以函数的单调减区间是,增区间是.

（2）因f(x)在上为减函数，故在上恒成立．

所以当时，．

又，

故当，即时，．

所以于是，故a的最小值为．

（3）命题“若使成立”等价于

“当时，有”．

由（Ⅱ），当时，，．

问题等价于：“当时，有”．

当时，由（Ⅱ），在上为减函数，

则=，故．

当时，由于在上为增函数，

故的值域为，即．

(i)若，即，在恒成立，故在上为增函数，

于是，=，不合题意．

(ii)若，即，由的单调性和值域知，

唯一，使，且满足：

当时，，为减函数；当时，，为增函数；

所以，=，．

所以，，与矛盾，不合题意．

综上，得．

知识点

函数的概念及其构成要素

1

题型：单选题

|

单选题 · 5 分

3.下列函数中，其图象既是轴对称图形又在区间（0，+∞）上单调递增的是（　　）

Ay=

B y=﹣x2+1

Cy=2x

Dy=lg|x+1

正确答案

D

解析

对于A，函数y=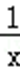的图象是中心对称图形，不是轴对称图形，∴不满足题意；

对于B，函数y=﹣x2+1的图象是轴对称图形，在区间（0，+∞）上是单调减函数，∴不满足题意；

对于C，函数y=2x的图象不是轴对称图形，∴不满足题意；

对于D，函数y=lg|x+1|的图象是关于直线x=﹣1对称的图形，且在区间（0，+∞）上是单调增函数，满足题意。

故选：D。

知识点

函数的概念及其构成要素

1

题型：单选题

|

单选题 · 5 分

2.函数的图象（）

A关于轴对称

B关于轴对称

C关于原点对称

D关于直线对称

正确答案

B

解析

∵余弦函数是偶函数,

∴函数是偶函数，故关于y轴对称，故选B.

知识点

函数的概念及其构成要素

1

题型：单选题

|

单选题 · 5 分

7.对于函数，若存在常数,使得取定义域内的每一个值，都有，则称为准偶函数，下列函数中是准偶函数的是 ( )

A

B

C

D

正确答案

A

解析

对于函数，若存在常数,使得取定义域内的每一个值，都有，则称为准偶函数，∴函数的对称轴是x=a，a≠0，

选项B、C、D函数没有对称轴；函数f（x）=cos（x+1），有对称轴，且x=0不是对称轴，选项A正确．

知识点

函数的概念及其构成要素

1

题型：填空题

|

填空题 · 5 分

11.定义在R上的函数f（x）满足f（x）=，则f（2013）的值为　　．

正确答案

﹣3

解析

由分段函数可知，当x＞0时，f（x）=f（x﹣1）﹣f（x﹣2），

∴f（x+1）=f（x）﹣f（x﹣1）=f（x﹣1）﹣f（x﹣2）﹣f（x﹣1），

∴f（x+1）=﹣f（x﹣2），

即f（x+3）=﹣f（x），

∴f（x+6）=f（x），即当x＞0时，函数的周期是6．

∴f（2013）=f（335×6+3）=f（3）=﹣f（0）=﹣log2（8﹣0）=﹣log28=﹣3，

故答案为：﹣3．

知识点

函数的概念及其构成要素

1

题型：简答题

|

简答题 · 12 分

17.在中，已知角A、B、C所对的边分别为a、b、c，直线与直线互相平行（其中）.

（1）求角A的值，

（2）若的取值范围.

正确答案

（1）；（2）

解析

（1）由得，

即，

所以，又,所以.

（2）

，

因为，所以，

所以，

即的取值范围为。

知识点

函数的概念及其构成要素

1

题型：填空题

|

填空题 · 4 分

15.已知函数（，，是常数，，）的部分图象如图所示．若，则．

正确答案

解析

由函数图像知：A=3，,所以,则；故，又过，解得，因为即，得，，故，则==

知识点

函数的概念及其构成要素

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点