- 函数概念与表示
- 共2805题
12.已知
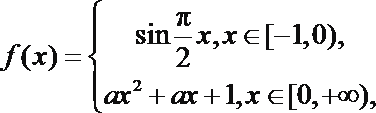
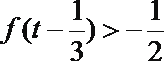
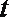
正确答案
(0,+∞)
解析
(0,+∞) 当x∈[-1,0)时,函数f(x)=sin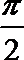




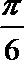







知识点
8.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.在




正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
7.为了得到函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知
(1)求f(x)的周期及其图象的对称中心;
(2)△ABC中,角A、B、C所对的边分别是


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.对于函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
选做题:请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.
22.选修4—1:几何证明选讲
如图,在正





(1)求证:
(2)若正

23.选修4—4;坐标系与参数方程.
已知曲线




(1)写出曲线

(2)求曲线

24.选修4-5:不等式选讲
已知函数
(1)解不等式
(2)设函数

22.选修4—1:几何证明选讲
如图,在正







⑴求证:
⑵若正

23.选修4—4;坐标系与参数方程.
已知曲线







⑴写出曲线

⑵求曲线



24.选修4-5:不等式选讲
已知函数
⑴解不等式
⑵ 设函数


正确答案
正确答案
正确答案
7.如图,一直线








正确答案
解析
A ∵












知识点
10. 已知函数

正确答案
0
解析
0 ∵由图形可知A=2,






知识点
扫码查看完整答案与解析
























