- 函数概念与表示
- 共2805题
17.已知函数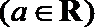
(Ⅰ)求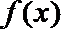
(Ⅱ)若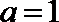
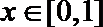
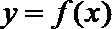
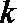
正确答案
解:(Ⅰ)函数的定义域为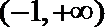
当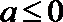
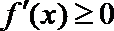

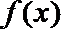
当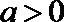
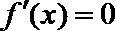
当
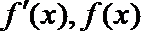
所以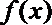
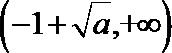
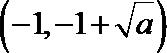
综上,当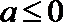
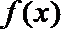
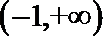
当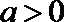
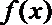
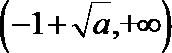
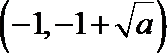
(Ⅱ)当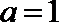
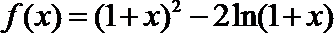
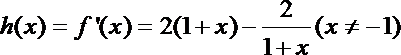
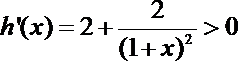
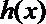
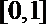
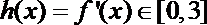
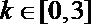
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数
(1)若

(2)若

正确答案
(1)解:
因为x = 2为f (x)的极值点,所以
即
又当a = 0时,


从而x = 2为f (x)的极值点成立.
(2)解:∵f (x)在区间[3,+∞)上为增函数,
∴
①当a = 0时,
②当a > 0时,
令

∵a > 0,∴
由

∵a > 0,∴
综上所述,a的取值范围为[0,
解析
解析已在路上飞奔,马上就到!
知识点
15、函数
正确答案
解析
知识点
13.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 设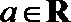
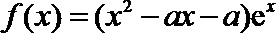
(Ⅰ)若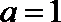
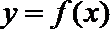
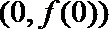
(Ⅱ)求函数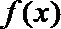
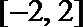
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.如果











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数
(I)若曲线


(II)求函数
(III)当a=1,且
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7、已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11、已知函数①y=sin x+cos x,②y=2
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析