- 诱导公式的推导
- 共118题
14.在锐角三角形


正确答案
8;
解析
由

可得
由三角形

在(*)式两侧同时除以

又
则
由

令


由(#)得






当且仅当


解得


考查方向
解题思路
根据诱导公式、和差角公式化简,利用两边同除得到正切关系,应用正切公式的变形分析表示出
易错点
公式变形,函数关系转化,函数思想应用。
知识点
5.若
正确答案
知识点
在

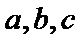
16.证明:
17.若

正确答案
由正弦定理得
故
于是
又




因此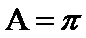

所以,
解析
见答案
考查方向
解题思路
先利用三角形正弦定理进行边角互化,再将角C用A,B表示,化简即可以得到结论
易错点
两正弦相等可能会缺少两角互补的情况
正确答案

解析
由
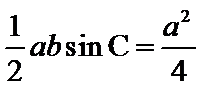

因




当



综上,

考查方向
解题思路
选择恰当的面积公式,进行边角互化。
易错点
两正弦相等可能会缺少两角互补的情况
21.【选做题】
在A、B、C、D四小题中只能选做两小题。解答时应写出文字说明、证明过程或演算步骤。
A.几何证明选讲
如图,从圆O外一点P作圆O的两条切线,切点分别为A,B,AB与OP交于点M,设CD为过点M且不过圆O的一条弦,求证:O、C、P、D四点共圆。
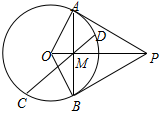
B.矩阵与变换
设矩阵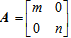
C.极坐标与参数方程
在极坐标系中,已知点O(0,0),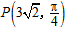
D.不等式选讲
设正实数a,b满足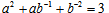
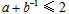
正确答案
A.
B.
C.
D.
解析
解析已在路上飞奔,马上就到!
知识点
6.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析