- 诱导公式的推导
- 共118题
甲、乙等五名大冬会志愿者被随机地分到黑大、体院、理工、亚布力四个不同的比赛场馆服务,每个场馆至少有一名志愿者。
(1)求甲、乙两人同时到黑大场馆服务的概率;
(2)设随机变量

正确答案
见解析
解析
(1)记甲、乙两人同时到黑大场馆服务为事件A,那么
即甲、乙两人同时到黑大场馆服务的概率是
(2)随机变量
事件“
则
所以


知识点
已知函数

(1)当

(2)若

(3)对于


证明:
正确答案
见解析
解析
(1)由

令





当



故

(2)



当

对于

当



当



于是

只需

∵



则



(3)解法1:
由已知得:

先证


设



∴

同理可证

解法2:
令

下面证明
令



构造函数






同理可证
即

得



同理,在区间


由
知识点
如图,四棱锥P-ABCD 的底面ABCD是正方形,PD⊥平面ABCD,E为PB上的点,且2BE=EP.
(1)证明:AC⊥DE;
(2)若PC=BC,求二面角E-AC-P的余弦值。
正确答案
见解析
解析
解析:解:(1)∵PD⊥平面ABCD,∴PD⊥AC,
∵底面ABCD是正方形,∴BD⊥AC,∴AC⊥平面PBD,
∵DE⊂平面PBD,∴AC⊥DE.(5分)
(2)以D为原点,DP,DA,DC所在的直线为x,y,z轴建立空间直角坐标系。
设BC=3,则CP=3,DP=3,因为2BE=EP,
易知D(0,0,0),A(0,3,0),C(0,0,3),P(3,0,0),E(1,2,2)。
所以→(CA)=(0,3,-3),→(CP)=(3,0,-3),→(CE)=(1,2,-1),
设平面ACP的法向量为u=(x,y,z),则u·→(CA)=0,u·→(CP)=0,
即3x-3z=0,(3y-3z=0,)令x=1,得u=(1,1,1),同理可取平面ACE的法向量v=(-1,1,1),
所以cos〈u,v〉=|u||v|(u·v)=3(1),由图知二面角E-AC-P为锐二面角,所以二面角E—AC—P的余弦值为3(1).(12分)
知识点
已知曲线C1的极坐标方程为ρcos(θ-
2

(1)求曲线C2的直角坐标方程;
(2)求曲线C2上的动点M到曲线C1的距离的最大值。
正确答案
见解析
解析
解析:
(1)
即

故

(2)

由(1)知曲线



所以动点

知识点
已知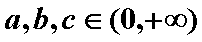
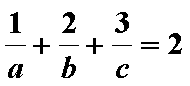
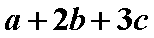
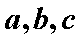
正确答案
见解析
解析
又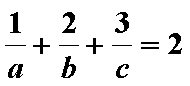
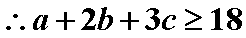
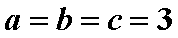
当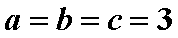
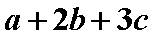
知识点
扫码查看完整答案与解析