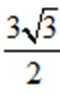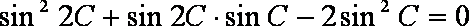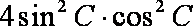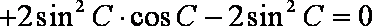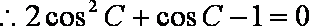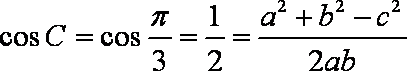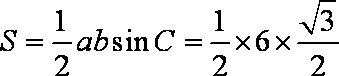- 诱导公式的推导
- 共118题
在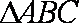
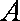
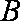
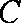
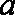
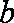
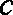
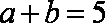
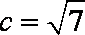
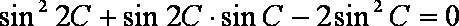
(1)求角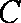
(2) 求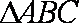
正确答案
(1)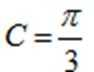
解析
(1)∵
∴
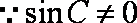
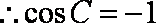
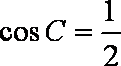
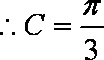
(2)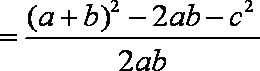
又∵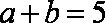
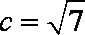
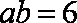
∴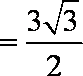
知识点
设集合




正确答案
解析
识别条件:
转念:这个集合中放的是点坐标! 满足
这个是啥东西? 是一个菱形,也是正方形,中心在坐标原点。 集合A中就是这个正方形内部的点。分象限逐一讨论 这个应该是平时练习过的一个知识点 还有比这个复杂的
继续识别条件:
继续识别条件:从集合





知识点
已知不等式2|x-3|+|x-4|<2a。
(1)若a=1,求不等式的解集;
(2)若已知不等式的解集不是空集,求a的取值范围。
正确答案
见解析
解析
解析:
(1)当

若



若


若


综上,不等式的解集为
(2)设





知识点
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,
(1)证明:面PBD⊥面PAC;
(2)求锐二面角A—PC—B的余弦值.
正确答案
见解析
解析
(1)因为四边形ABCD是菱形,
所以AC
因为PA
所有PA
又因为PA
所以BD
而BD
所以面PBD
(2)如图,设AC
在△APC中,AO=OC,CQ=QP,OQ为△APC的中位线,所以OQ//PA.
因为PA
所以OQ
以OA、OB、OQ所在直线分别为

则

因为BO
所以平面PAC的一个法向量为
设平面PBC的一个法向量为
而
由
令
所以



知识点
如图,在空间中的直角三角形ABC与直角梯形EFGD中,平面ABC//平面DEFG,AD⊥平面DEFG,AC∥DG.且AB=AD=DE=DG=2,AC=EF=1.
(1)求证:四点B、C、F、G共面;
(2)求平面ADGC与平面BCGF所组成的二面角余弦值;
(3) 求多面体ABC-DEFG的体积.
正确答案
见解析
解析
由 AD⊥面DEFG和直角梯形EFGD可知,AD、DE、DG两两垂直,建立如图的坐标系,则A(0,0,2),B(2,0,2),C(0,1,2),E(2,0,0),G(0,2,0),F(2,1,0)
(1)
∴
故四点B、C、F、G共面. ……………………4分
(2)
设平面BC

则
令

而平面ADGC的法向量
∴

故面ADGC与面BCGF所组成的二面角余弦值为
(3)设DG的中点为M,连接AM、FM,则
=


解法二 (1)设DG的中点为M,连接AM、FM,则由已知条件易证四边形DEFM是平行四边形,所以MF//DE,且MF=DE
又∵AB//DE,且AB=DE ∴MF//AB,且MF=AB
∴四边形ABMF是平行四边形,即BF//AM,且BF=AM

∴AC//MG,且AC=MG,即四边形ACGM是平行四边形
∴GC//AM,且GC=AM
故GC//BF,且GC=BF,
即四点B、C、F、G共面………………4分
(2)∵四边形EFGD是直角梯形,AD⊥面DEFG
∴DE⊥DG,DE⊥AD,即DE⊥面ADGC ,
∵MF//DE,且MF=DE , ∴M
在平面ADGC中,过M作MN⊥GC,垂足为N,连接NF,则
显然∠MNF是所求二面角的平面角.
∵在四边形ADGC中,AD⊥AC,AD⊥DG,AC=DM=MG=1
∴



∴
在直角三角形MNF中,MF=2,MN
∴




故面ADGC与面BCGF所组成的二面角余弦值为
(3)




知识点
扫码查看完整答案与解析