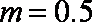- 函数解析式的求解及常用方法
- 共177题
14.已知函数f(x)=
正确答案

解析
依题意得,f1(x)=
f2(x)=


f3(x)=


由此归纳可得fn(x)=
知识点
16.已知函数
(1)求函数
(2)设



正确答案
(1)
(2)
解析
(1)由图象可知



(2)∵

又∵

∵

∴
知识点
某地政府鉴于某种日常食品价格增长过快,欲将这种食品价格控制在适当范围内,决定对这种食品生产厂家提供政府补贴,设这种食品的市场价格为







(1)将政府补贴表示为市场平衡价格的函数,并求出函数的值域;
(2)为使市场平衡价格不高于每千克20元,政府补贴至少为每千克多少元?
正确答案
(1)[



(2)政府补贴至少为1.5元/千克
解析
(1)由P=Q得2(x + 4t -14 )= 24+8ln
t=














tmax=









(2)由(1) t=


而x=20时,t=





要使市场平衡价格不高于每千克20元,政府补贴至少为1.5元/千克。
知识点
5.已知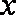
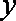
已求得关于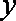

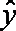
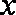
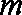
正确答案
解析

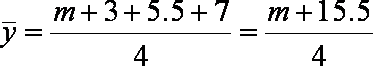
因为回归直线过点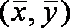
所以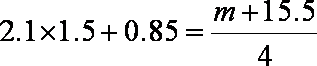
解得:
故选:D
知识点
20.函数





(1)求

(2)求

(3)若函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知平面向量a=(

(1)证明a⊥b;
(2)若存在不同时为零的实数k和t,使x=a+ (t2–3)b,y=–ka+tb,且x⊥y,试求函数关系式k=f(t);
(3)据(2)的结论,讨论关于t的方程f(t)–k=0的解的情况。
正确答案
(1)证明:∵a·b=
(2)解:∵x⊥y,∴x·y=0
即[a+(t2–3)b]·(–ka+tb)=0,整理后得
–ka2+[t–k(t2–3)]a·b+t(t2–3)·b2=0
∵a·b=0,a2=4,b2=1
∴上式化为–4k+t(t2–3)=0,∴k=
(3)解:讨论方程

于是f′(t)=

令f′(t)=0,解得t1=–1,t2=1.当t变化时,f′(t),f(t)的变化情况如下表:
当t=–1时,f(t)有极大值,f(t)极大值=
当t=1时,f(t)有极小值,f(t)极小值=–
而f(t)=


所以f(t)的图象大致如下:
于是当k>

当k=



解析
解析已在路上飞奔,马上就到!
知识点
17、解答应写出文字说明、证明过程或演算步骤。
(1)不用计算器计算:log3
(2)如果f(x-

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.已知函数



(1)求
(2)若函数




(3)若







正确答案
(1)把
分别代入
可得:
化简此方程组
可得:
即
可得

代入原方程组可得:
(2)由题意知:



即







又


(3)由

即










又
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知:二次函数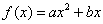
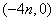
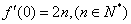
(1)求: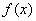
(2)若数列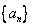
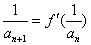
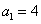
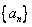
(3)对于(2)中的数列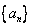
①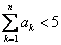
②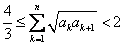
正确答案
解:(1)由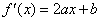
∴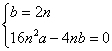
解得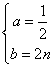
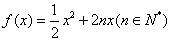
(2)∵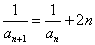
∴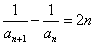
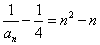
∴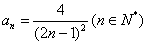
(3)①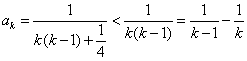
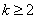
当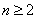
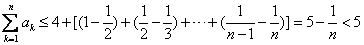
②∵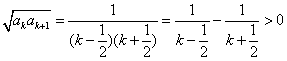
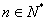
∴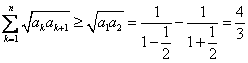
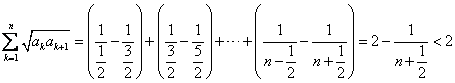
即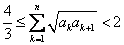
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析