- 函数解析式的求解及常用方法
- 共177题
13.若函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.统计表明,某种型号的汽车在匀速行驶中每小时耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为:y=
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知:二次函数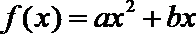

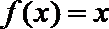
(1)求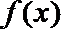
(2)是否存在实数m、n,(m<n),使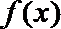
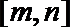
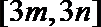
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 设二次函数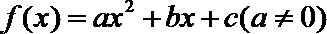
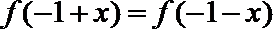
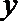
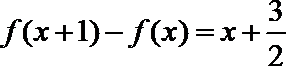
(1)求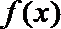
(2)若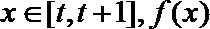
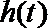
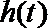
(3)若不等式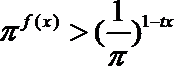
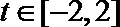
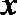
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知A(






(1)求



(2)已知






(3)在(2)的条件下,设









正确答案
解:
(1)∵点M在直线x=

又



∴

① 当






② 当







综合①②得,

(Ⅱ)由(Ⅰ)知,当


∴

n≥2时,




①+②得,2

当n=1时,


(Ⅲ)













∴

当c=1时,
∴1<
∴m=1.
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,ABCD是正方形空地,边长为30m,电源在点P处,点P到边AD,AB距离分别为



(1)求S关于x的函数关系式及该函数的定义域;
(2)当x取何值时,液晶广告屏幕MNEF的面积S最小?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知


(1) 求
(2)若对任意

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.定义一个对应法则







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.为了加强环保建设,提高社会效益和经济效益,长沙市计划用若干时间更换一万辆燃油型公交车,每更换一辆新车,则淘汰一辆旧车,替换车为电力型和混合动力型车.今年初投入了电力型公交车128辆,混合动力型公交车400辆;计划以后电力型车每年的投入量比上一年增加50%,混合动力型车每年比上一年多投入a辆.
(1)求经过n年,该市被更换的公交车总数S(n);
(2)若该市计划7年内完成全部更换,求a的最小值.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析