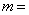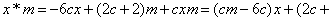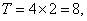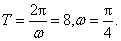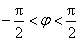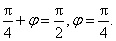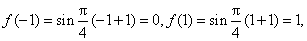- 函数解析式的求解及常用方法
- 共177题
某企业计划投资A,B两个项目, 根据市场分析,A,B两个项目的利润率分别为随机变量X1和X2,X1和X2的分布列分别为:
(1)若在A,B两个项目上各投资1000万元,Y1和Y2分别表示投资项目A和B所获得的利润,求利润的期望

(2)由于资金限制,企业只能将x(0≤x≤1000)万元投资A项目,1000-x万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和,求f(x)的最小值,并指出x为何值时,f(x)取到最小值。
正确答案
见解析。
解析
(1)由题设可知Y1和Y2的分布列为
--------------2分
E(Y1)=50×0.8+100×0.2=60,----------------------------------3分
D(Y1)=(50-60)2×0.8+(100-60)2×0.2=400,------------------------4分
E(Y2)=20×0.2+80×0.5+120×0.3=80,---------------------------------------5分
D(Y2)=(20-80)2×0.2+(80-80)2×0.5+(120-80)2×0.3=1200.-------------------6分
(2)
=

当
知识点
对任意实数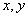
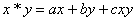
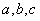
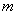
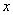
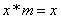
正确答案
解析
由定义可知,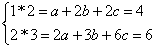
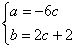
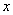
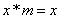
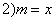
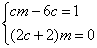
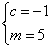
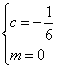
知识点
已知


正确答案
1
解析
二项展开式的通项为







知识点
已知函数
为
(1)求
(2)求


正确答案
见解析。
解析
(1)




(2)


当


当


知识点
已知函数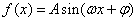
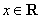
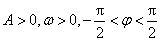
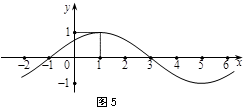
(1)求函数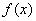
(2)已知横坐标分别为-1、1、5的三点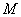
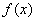
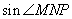
正确答案
见解析。
解析
(1)由图可知,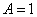
最小正周期
所以
又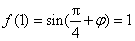
所以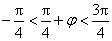
所以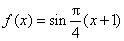
(2)解法一: 因为
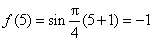
所以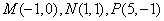
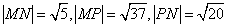
从而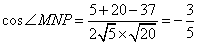
由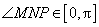
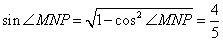
解法二: 因为
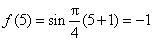
所以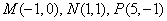
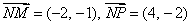
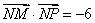
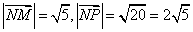
则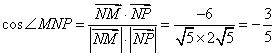
由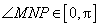
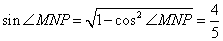
知识点
某学校每星期一供应1000名学生A、B两种菜。调查表明,凡在这星期一选A种菜的,下星期一会有




(1)若


(2)求
正确答案
见解析。
解析
(1)

(2)


所以





随着时间推移,即





知识点
已知函数

(1)求函数
(2)求函数

正确答案
见解析。
解析
(1)

因此,函数

(2)由题易知

在区间
又


所以,函数


知识点
设函数

(1)当





(2)若函数

正确答案
见解析。
解析
(1)由题易得

因为直线

则令



易得,







①当





②当

则

令

易得方程(*)在




所以直线

综上所述,直线


(2)由题易知,



即



即
设






所以
所以当

要使



综上所述,若


知识点
设二次函数




(1)求函数
(2)试写出一个区间


(3)已知



正确答案
见解析
解析
(1)由

从而得:



其值域为
(2)解:当

设




从而得



注:本题的区间也可以是


另解:若数列
即
又当






(3)由(2)知



令


从而有




从而得


所以

所以

知识点
已知




(1)求
(2)设




正确答案
见解析
解析
(1)如图,在


可得
又 


则函数

其中定义域为
说明:亦可用积化和差方法化简:

(2)
由


1




2




因而存在实数


知识点
扫码查看完整答案与解析