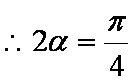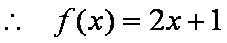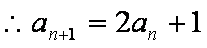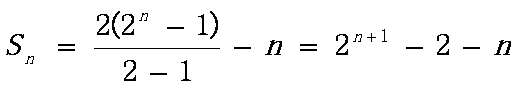- 函数解析式的求解及常用方法
- 共177题
设区间(0,1)内的实数





正确答案


解析
如图设圆心为O1,圆O1的半径为
设M的坐标为
则
当点m在Q点下方时同理可得
又点A(0,1)
∴直线AM的方程为:
即:
令
知识点
已知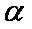
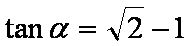
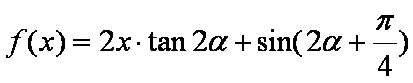
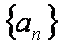
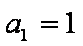
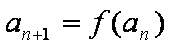
(1)求函数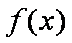
(2)求数列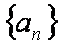
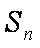
正确答案
(1)
解析
(1)由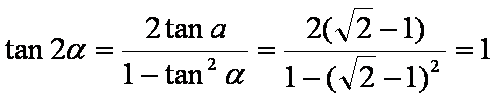
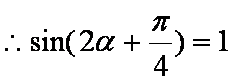
(2)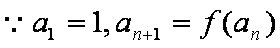
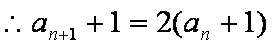

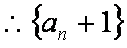
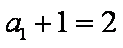
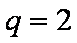
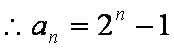
∴
知识点
设函数f(x)=g(x)+x2,曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,则曲线y=f(x)在点(1,f(1))处切线的斜率为( )
正确答案
解析
f′(x)=g′(x)+2x。
∵ y=g(x)在点(1,g(1))处的切线方程为y=2x+1,
∴ g′(1)=2,∴f′(1)=g′(1)+2×1=2+2=4,
∴ y=f(x)在点(1,f(1))处切线斜率为4。
故选A。
知识点
十字路口车流量被定义为单位时间内通过十字路口的车辆数,小张上班经过的某十字路口某时间段内



正确答案
解析
略
知识点
已知函数

正确答案
解析
由图可知
∴T=3
∴
知识点
经市场调查,某旅游城市在过去的一个月内(以30天计),第t天(1≤t≤30, t∈N﹢)的旅游人数


(1)求该城市的旅游日收益w(t)(万元)与时间t(1≤t≤30,t∈N﹢)的函数关系式;
(2)求该城市旅游日收益的最小值。
正确答案
(1)
(2)441万元
解析
(1)
=
(2)当

当


所以
知识点
已知函数y=f(x)在定义域(—1+∞)内满足f(o)=0,且f/(x)=
(1)求f(x)的表达式.
(2)当a=1时,讨论f(x)的单调性
(3)设h(x)=(ex—P)2+(x-P)2,证明:h(x)≥
正确答案
见解析
解析
解析:(1)由f/(x)=


(2)当a=1时,f(x)= ln(1+x)—x. (x>-1)
f/(x)=
由f/(x)=0
当x∈(0,+∞)时,f/(x)<0,此时f(x)递减
即f(x)在(-1,0)上单调增,在(0,+∞)上单调减…………………………8分
(Ⅲ)由(Ⅱ)知f(x)≤f(0)=0在(-1,+∞)内恒成立
∴ln (1+x) ≤x
∴ex≥1+x 
∴≤
即h(x)=(ex-P)2+(P-x)2≥
知识点
某餐厅的原料费支出

正确答案
解析
略
知识点
设x1,x2(x1≠x2)是函数f(x)=ax3+bx2﹣a2x(a>0)的两个极值点。
(1)若x1=-1,x2=2,求函数f(x)的解析式;
(2)若
(3)若x1<x<x2,且x2=a,g(x)=f'(x)﹣a(x﹣x1),求证:
正确答案
见解析。
解析
(1)求导函数,可得f′(x)=3ax2+2bx﹣a2,
∵x1=﹣1,x2=2是函数f(x)的两个极值点,
∴f'(﹣1)=0,f'(2)=0,
∴3a﹣2b﹣a2=0,12a+4b﹣a2=0,
解得a=6,b=﹣9。
∴f(x)=6x3﹣9x2﹣36x,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(4分)
(2)∵x1,x2是函数f(x)的两个极值点,∴f'(x1)=f'(x2)=0。
∴x1,x2是方程3ax2+2bx﹣a2=0的两根,故有△=4b2+12a3>0对一切a>0,b∈R恒成立。
∴
∵a>0,∴x1•x2<0,
∴
由

∴b2=3a2(6﹣a)。
∵b2≥0,∴3a2(6﹣a)≥0,∴0<a≤6。
令h(a)=3a2(6﹣a),则h′(a)=36a﹣9a2。
当0<a<4时,h′(a)>0,∴h(a)在(0,4)内是增函数;
当4<a<6时,h′(a)<0,∴h(a)在(0,4)内是减函数;
∴当a=4时,h(a)是极大值为96,
∴h(a)在(0,6)上的最大值是96,∴b的最大值是
(3)∵x1,x2是方程3ax2+2bx﹣a2=0的两根。∴f'(x)=3a(x﹣x1)(x﹣x2)
∵
∴
∵x1<x<x2,
∴
=﹣3a
知识点
如图是函数f(x)=x2+ax+b的部分图象,则函数g(x)=lnx+f′(x)的零点所在的区间是
正确答案
解析
由函数f(x)=x2+ax+b的部分图象得0<b<1,f(1)=0,从而﹣2<a<﹣1,
而g(x)=lnx+2x+a在定义域内单调递增,
g(

g(1)=ln1+2+a=2+a>0,
∴函数g(x)=lnx+f′(x)的零点所在的区间是(
知识点
扫码查看完整答案与解析