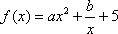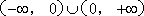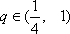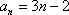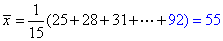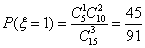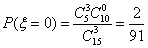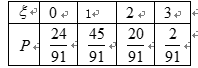- 二项式系数的和或各项系数的和问题
- 共73题
在



正确答案
解析
令





知识点

正确答案
-20
解析
略
知识点
小明有4枚完全相同的硬币,每个硬币都分正反两面.他想把4个硬币摆成一摞,且满足相邻两枚硬币的正面与正面不相对,不同的摆法有()
正确答案
解析
略
知识点
已知函数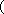
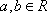
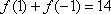
(1)求出
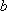
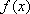
(2)若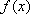
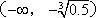
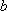
(3)在(2)的条件下,当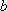
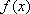
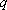
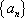
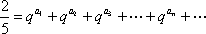
正确答案
见解析
解析
(1)由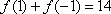
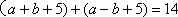

从而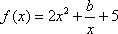
当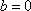

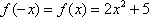
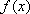
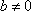
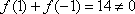
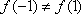
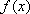
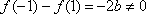
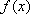
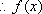
(2)对于任意的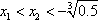
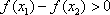
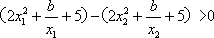
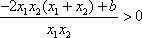
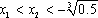
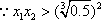
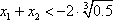
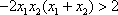
又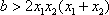

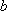
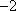
(3)在(2)的条件下,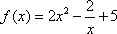
当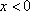
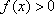
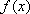
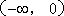
当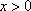
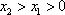
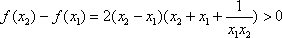
即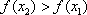
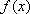
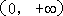
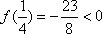
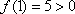
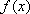
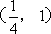
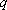
综上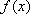
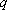
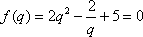
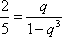
又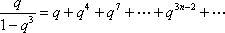
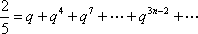
知识点
二项式
正确答案
9
解析
略
知识点
PM2. 5是指大气中直径小于或等于2. 5微米的颗粒物,也称为可入肺颗粒物。 虽然PM2.5只是地球大气成分中含量很少的组分,但它对空气质量和能见度等有重要的影响。我国PM2. 5标准如表1所示.我市环保局从市区四个监测点2012年全年每天的PM2.5监测数据中随机抽取15天的数据作为样本,监测值如茎叶图如图4所示。
(1)求这15天数据的平均值(结果保留整数)。
(2)从这15天的数据中任取3天的数据,记表示其中空气质量达到一级的天数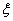
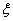
(3)以这15天的PM2. 5日均值来估计一年的空气质量情况,则一年(按360天计算)中大约有多少天的空气质量达到一级。
正确答案
见解析。
解析
(1)随机抽取15天的数据的平均数为:
(2)依据条件, 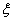
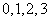
当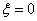
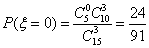
当
当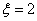
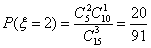
当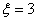
所以其分布列为:
数学期望为:
(3)依题意可知,一年中每天空气质量达到一级的概率为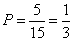
一年中空气质量达到一级的天数为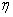
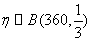
∴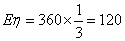
所以一年中平均有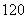
知识点
若将函数
其中




正确答案
10
解析
法一:由等式两边对应项系数相等。
即:
法二:对等式:




知识点
二项式(1+sinx)n的展开式中,末尾两项的系数之和为7,且系数最大的一项的值为

正确答案
解析
略。
知识点
椭圆





(1)求椭圆
(2)点







(3)在(2)的条件下,过








正确答案
见解析。
解析
(1)由于


由题意知

所以

(2)由题意可知:







所以

(3)由题意可知,l为椭圆的在p点处的切线,由导数法可求得,切线方程为:





知识点
有两个同心圆,在外圆周上有不重合的六个点,在内圆周上有不
重合的三个点,由这九个点确定的直线最少有
正确答案
解析
略
知识点
扫码查看完整答案与解析