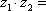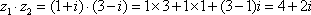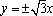- 诱导公式的作用
- 共120题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知数列{an}的前n项和为Sn,a1=1,an≠0,anan+1=λSn-1,其中λ为常数。
(1)证明:an+2-an=λ.
(2)是否存在λ,使得{an}为等差数列?并说明理由。
正确答案
见解析。
解析
(1)证明:由题设,anan+1=λSn-1,an+1an+2=λSn+1-1,
两式相减得an+1(an+2-an)=λan+1.
因为an+1≠0,所以an+2-an=λ.
(2)由题设,a1=1,a1a2=λS1-1,可得 a2=λ-1,
由(1)知,a3=λ+1.
若{an}为等差数列,则2a2=a1+a3,解得λ=4,故an+2-an=4.
由此可得{a2n-1}是首项为1,公差为4的等差数列,
a2n-1=4n-3;
{a2n}是首项为3,公差为4的等差数列,a2n=4n-1.
所以an=2n-1,an+1-an=2.
因此存在λ=4,使得数列{an}为等差数列。
知识点
若复数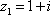
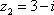
正确答案
解析
知识点
若变量 x,y满足约束条件
正确答案
1
解析
不等式的解法及应用。
作出不等式对应的平面区域,利用线性规划的知识,通过平移即可求z的最小值。
作出不等式对应的平面区域如图,
由z=3x+y,得y=﹣3x+z,
平移直线y=﹣3x+z,由图象可知当直线y=﹣3x+z,经过点A(0,1)时,直线y=﹣3x+z的截距最小,
此时z最小,此时z的最小值为z=0×3+1=1,
知识点
“

正确答案
解析
由

(或由



知识点
i为虚数单位,则
正确答案
解析

知识点
已知a,b是实数,函数f(x)=x3+ax,g(x)=x2+bx, f ′(x)和g′(x)分别是f(x)和g(x)的导函数.若f ′(x)g′(x)≥0在区间I上恒成立,则称f(x)和g(x)在区间I上单调性一致。
(1)设a>0.若f(x)和g(x)在区间[-1,+∞)上单调性一致,求b的取值范围;
(2)设a<0且a≠b.若f(x)和g(x)在以a,b为端点的开区间上单调性一致,求|a-b|的最大值。
正确答案
(1)x=±
(2)
解析
f ′(x)=3x2+a,g′(x)=2x+b.
(1)由题意知f ′(x)g′(x)≥0在[-1,+∞)上恒成立。
因为a>0,故3x2+a>0,进而2x+b≥0,即b≥-2x在区间[-1,+∞)上恒成立,
所以b≥2.因此b的取值范围是[2,+∞)。
(2)令f ′(x)=0,解得x=±
若b>0,由a<0得0∈(a,b).又因为f ′(0)g′(0)=ab<0,所以函数f(x)和g(x)在(a,b)上不是单调性一致的.因此b≤0.
现设b≤0.当x∈(-∞,0)时,g′(x)<0;
当x∈
当x∈
故由题设得a≥-

从而-

因此|a-b|≤

又当a=-




知识点
已知双曲线
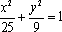
正确答案
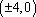
解析
双曲线焦点即为椭圆焦点,不难算出为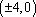
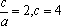
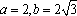
知识点
扫码查看完整答案与解析