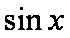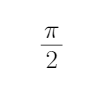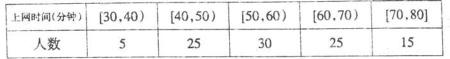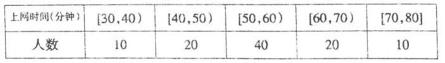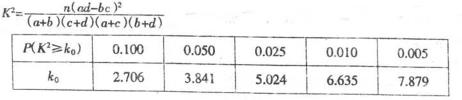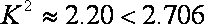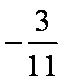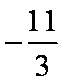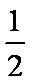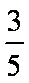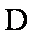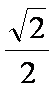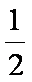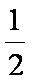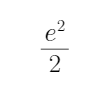- 诱导公式的作用
- 共120题
函数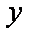
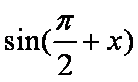
正确答案
解析
略
知识点
已知
cosA=

(1)求tanC的值;
(2)若a=

正确答案
见解析
解析
(1)∵cosA=

又
=

整理得:tanC=
(2)由(1)知sinC=
由正弦定理知:

又∵sinB=

∴


知识点
某音乐喷泉喷射的水珠呈抛物线形,它在每分钟内随时间






(1)试求此喷泉喷射的圆形范围的半径最大值;
(2)若在一建筑物前计划修建一个矩形花坛并在花坛内装置两个这样的喷泉,则如何设计花坛的尺寸和两个喷水器的位置,才能使花坛的面积最大且能全部喷到水?
正确答案
见解析。
解析
(1)当
因


从而当


所以此喷泉喷射的圆形范围的半径最大值是
(2)设花坛的长、宽分别为xm,ym,根据要求,矩形花坛应在喷水区域内,顶点应恰好位于喷水区域的边界,依题意得:

问题转化为在


法一:





法二:∵


∴当




答:花坛的长为

知识点
为了调査某大学学生在某天上网的时间,随机对lOO名男生和100名女生进行了不记名的问卷调查.得到了如下的统计结果:
表1:男生上网时间与频数分布表
表2:女生上网时间与频数分布表
(1)从这100名男生中任意选出3人,其 中 恰 有 1人上网时间少于60分钟的概率;
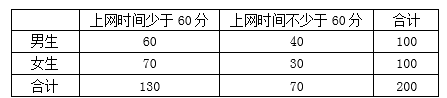
(2)完 成 下 面 的 2X2列 联 表,并 回 答 能 否 有 90%的 把 握 认 为 “大 学 生 上 网 时 间 与 性 别 有 关 ”?
表3:
附:
正确答案
见解析
解析
解析:(1)由男生上网时间频数分布表可知100名男生中,上网时间少于60分钟的有60人,不少于60分钟的有40人,………………2分
故从其中任选3人,恰有1人上网的时间少于60分钟的概率为
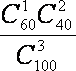
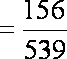
(2)
……………8分
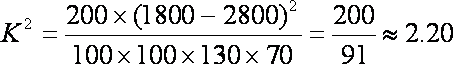
∵
∴没有90%的把握认为“大学生上网时间与性别有关”.………………12分
知识点
已知点



(1)若


(2)若




正确答案
见解析
解析
(1)当

所以可设直线


∴
得:
∴直线
∵


∴
∵



∴直线

(2)由(1)可知


因为直线
∴


由


∴





即
此时直线

法二:
(1)根据题意设


由



由

∴直线

(2)由(1)知直线




点


由
当



知识点
已知

正确答案
解析
略
知识点
已知向量





正确答案
1
解析
知识点
已知向量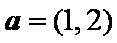
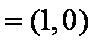
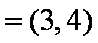
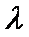
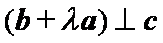
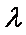
正确答案
解析
函数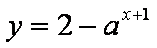
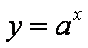

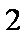
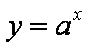
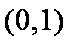
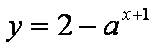
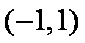
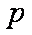
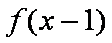
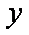
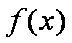
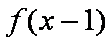
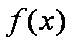
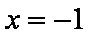
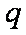
知识点
在ABC中,若tanAtanB= tanA+ tanB+ 1,则cosC的值是
正确答案
解析
由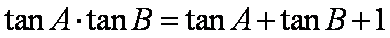
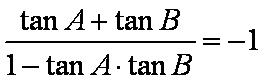
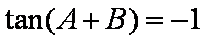
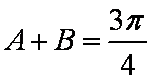
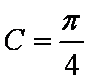
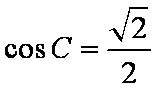
知识点
若曲线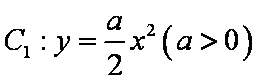
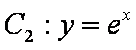
正确答案
a ≥
解析
略
知识点
扫码查看完整答案与解析