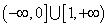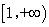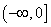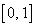函数的单调性及单调区间
共89题

· 函数的单调性及单调区间

函数的单调性及单调区间
共89题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

函数f（x）在[a，b]上有定义，若对任意x1，x2∈[a，b]，有则称f（x）在[a，b]上具有性质P，设f（x）在[1，3]上具有性质P，现给出如下命题：

①f（x）在[1，3]上的图象是连续不断的；

②f（x2）在[1，]上具有性质P；

③若f（x）在x=2处取得最大值1，则f（x）=1，x∈[1，3]；

④对任意x1，x2，x3，x4∈[1，3]，有[f（x1）+f（x2）+f（x3）+f（x4）]

其中真命题的序号是（　　）

A①②

B①③

C②④

D③④

正确答案

解析

在①中，反例：f（x）=在[1，3]上满足性质P，

但f（x）=在[1，3]上不是连续函数，故①不成立；

在②中，反例：f（x）=﹣x在[1，3]上满足性质P，但f（x2）=﹣x2在[1，]上不满足性质P，

故②不成立；

在③中：在[1，3]上，f（2）=f（）≤，

∴，

故f（x）=1，

∴对任意的x1，x2∈[1，3]，f（x）=1，

故③成立；

在④中，对任意x1，x2，x3，x4∈[1，3]，

有=

≤

=[f（x1）+f（x2）+f（x3）+f（x4）]，

∴[f（x1）+f（x2）+f（x3）+f（x4）]，

故④成立。

知识点

函数的单调性及单调区间

题型：填空题

填空题 · 5 分

设是定义在上且周期为2的函数，在区间上，其中，若，则的值为（）。

正确答案

-10

解析

∵是定义在上且周期为2的函数，∴，即①。

又∵，，

∴②。

联立①②，解得，。∴。

知识点

函数的单调性及单调区间

题型：简答题

简答题 · 13 分

已知函数

（1）若函数在处有极值为10，求b的值；

（2）若对于任意的，在上单调递增，求b的最小值。

正确答案

（1）

（2）的最小值为

解析

（1），　　　　　　　　……………………………… 1分

于是，根据题设有

解得或 ……………………3分

当时，，，所以函数有极值点； ………………………………………………………………4分

当时，，所以函数无极值点，……………5分

所以　，………………………………………………………………6分

（2）法一：对任意，都成立，………7分

所以对任意，都成立…8分

因为 ,

所以在上为单调递增函数或为常数函数， ………9分

所以对任意都成立 …10分

即 . …………………………………………11分

又，

所以　当时，，………………………………12分

所以　，

所以　的最小值为， ………………………………13分

法二：对任意，都成立， ……………7分

即对任意，都成立，

即， …………………………………………8分

令，………………………………9分

当时，，于是；…………………………10分

当时，，于是，，………11分

又，所以。 ………………………………12分

综上，的最小值为。 ………………………………13分

知识点

函数的单调性及单调区间

题型：简答题

简答题 · 13 分

已知函数。

（1）求的最小正周期；

（2）求函数在的最大值和最小值。

正确答案

（1）

（2）最大值；最小值

解析

（1）由已知，得

……………………2分

， ……………………4分

所以　，

即的最小正周期为； ……………………6分

（2）因为　，所以　。 ……………… 7分

于是，当时，即时，取得最大值；…… 10分

当时，即时，取得最小值，……………13分

知识点

函数的单调性及单调区间

题型：单选题

单选题 · 5 分

函数的定义域为,若存在非零实数，使得对于任意有且，则称为上的度低调函数，已知定义域为的函数，且为上的度低调函数，那么实数的取值范围是（）

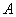
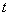
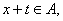
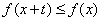
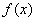
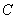
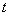
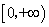
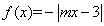
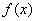
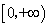
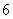
正确答案

解析

略。

知识点

函数的单调性及单调区间

继续学习学习下一知识点

下一知识点 : 函数单调性的判断与证明

百度题库 > 高考 > 理科数学 > 函数的单调性及单调区间

扫码查看完整答案与解析