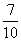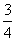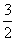- 函数的单调性及单调区间
- 共89题
定义在







正确答案
0
解析
略
知识点
(1)已知






(2)求函数

正确答案
见解析
解析
(1)作差比较:


所以,

当
(2)解法1:
当


解法2:


设


因为
当且仅当











知识点
定义函数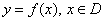
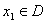
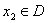
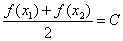
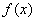
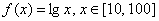
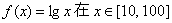
正确答案
解析
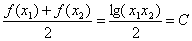
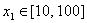
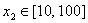
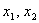
令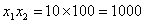
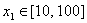
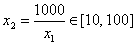
由此得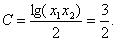
知识点
已知函数


(1)若

(2)若对任意




(3)在第(2)问求出的实数






正确答案
见解析
解析
解:(1)当


由





(2)易知
依题意知

因为



(3)解法一:易知

显然

①当


令

此时


②当


令

此时




由于



解法二:对任意



由(2)可知实数
故

①当


∴
要使
若

若

解得
故

②当




要使

解得
或

综上所述,当


知识点
已知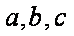
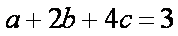
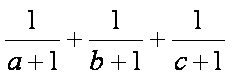
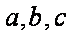
正确答案
见解析。
解析
因为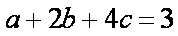
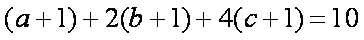
因为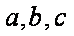
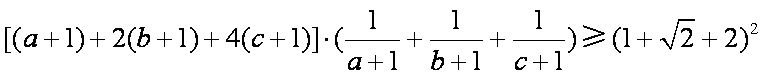
当且仅当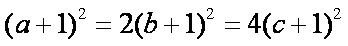
所以
所以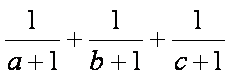
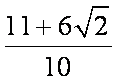
此时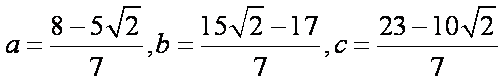
知识点
扫码查看完整答案与解析