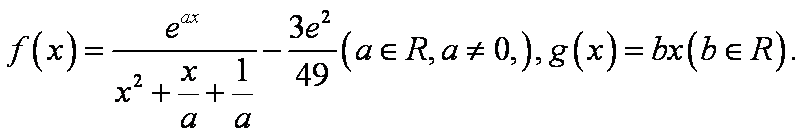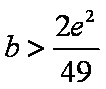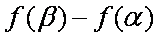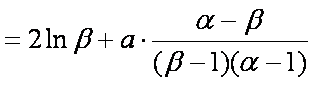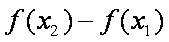- 函数的单调性及单调区间
- 共89题
设函数

(1)讨论
(2)若








正确答案
见解析
解析
(1)
令
当

故f(x)在(0,+
当



故f(x)在(0,+
当



当


当

故f(x)分别在


(2)由(1)知

又由(1)知,

若存在m,使得
即
即

再由(1)知,函数
在


这与(*)式矛盾,故不存在m,使得
知识点
已知函数
(1)求此函数的单调区间及最值;
(2)求证:对于任意正整数n,均有

(3)当a=1时,是否存在过点(1,-1)的直线与函数
正确答案
见解析
解析
解析:(1)由题意
当


此时函数在


当


此时函数在


(2)取

故
取

(3)假设存在这样的切线,设其中一个切点
∴切线方程:



设






故
又
注意到


方程①有且仅有一解,故符合条件的切线有且仅有一条…………14分
知识点
已知函数
(1)当
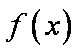
(2)当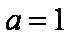
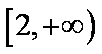
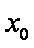
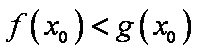
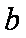
正确答案
见解析
解析
解析:(1)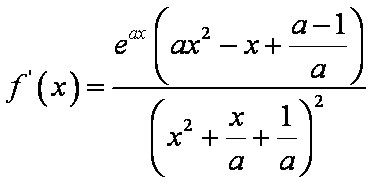
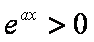
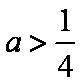
故只需讨论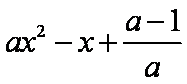
所以 ① 当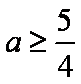
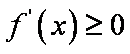
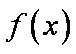
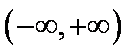
② 当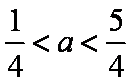
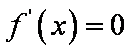
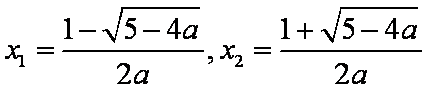
当x变化时, f '(x)和f(x)的变化情况如下表:
∴f(x)在
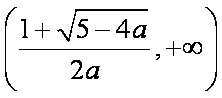

(2)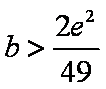
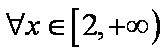
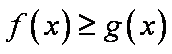
即
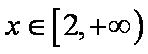
首先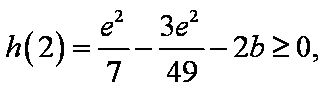
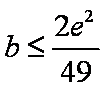
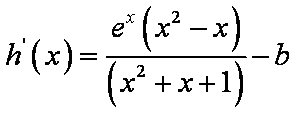
考虑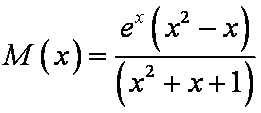

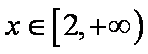
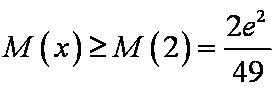
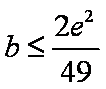
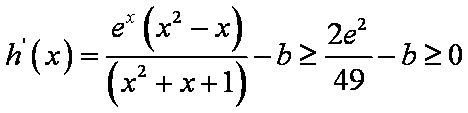
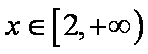
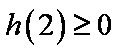

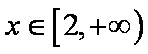
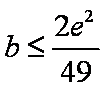
综上
知识点
设函数f(x)=(x+2)2-2ln(x+2)。
(1)求f(x)的单调区间;
(2)若关于x的方程f(x)=x2+3x+a在区间[-1,1]上只有一个实数根,求实数a的取值范围。
正确答案
见解析
解析
解析:(1)函数


所以 当



故


(注: -1处写成“闭的”亦可)
(2)由

令

所以



故


要使方程

解之得
所以实数

知识点
设函数f (x)=ln x+

(1) 求实数a的取值范围;
(2)若x1∈(0,1),x2∈(1,+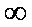

(注:e是自然对数的底数)
正确答案
见解析
解析
(1)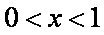
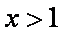
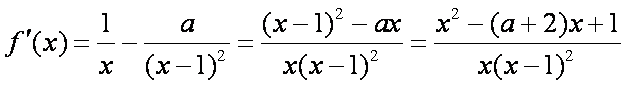
由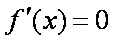
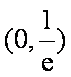

不妨设
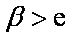

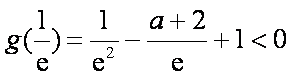
解得
(2)由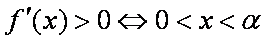
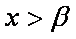
由
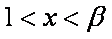
得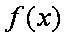
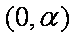
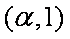
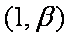
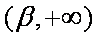
由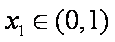
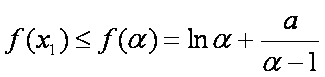
由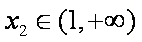

所以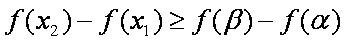
因为
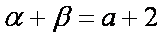
所以
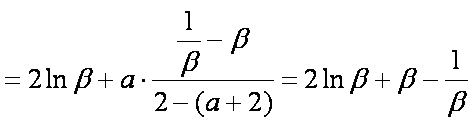
记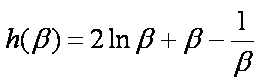
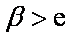
则
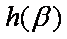
所以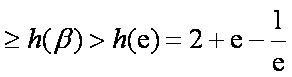
知识点
扫码查看完整答案与解析