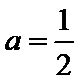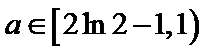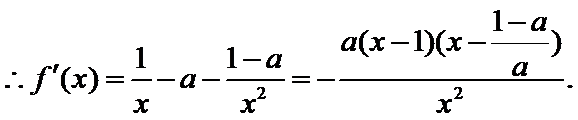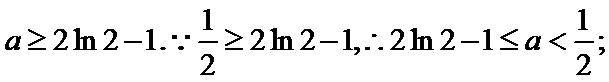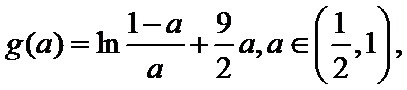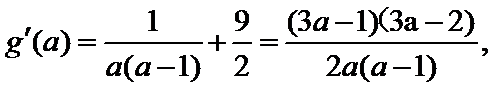- 函数的单调性及单调区间
- 共89题
10. 设



正确答案
解析
由已知,

知识点
设函数
25.讨论函数

26.记


27.在(Ⅱ)中,取


正确答案
(Ⅰ)极小值为
解析
(Ⅰ)



因为

①当

②当

③当







因此,




考查方向
解题思路
(Ⅰ)将



求导得





















易错点
函数求导错误,分类讨论能力弱,计算能力弱
正确答案
解析
:
(Ⅱ)

当

当

由此可知,函数


考查方向
解题思路
当




易错点
绝对值不等式性质运用错误,计算错误,不会合理放缩不等式
正确答案
(Ⅲ)1.
解析
(Ⅲ)



取


由此可知,

考查方向
解题思路
(Ⅲ)当








易错点
平均值不等式的性质,计算能力弱
20.(本小题满分13分)
已知
(I)讨论
(II)当


正确答案
知识点
3.下列函数中,既不是奇函数,也不是偶函数的是
正确答案
解析
令








考查方向
解题思路
逆带验证排除法。代入特殊值,对选项进行检验即可选出答案。
易错点
定义域关于原点对称是函数具有奇偶性的前提,奇函数、偶函数的表达式满足的关系不要弄错。
知识点
已知函数f(x)=lnx-ax+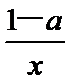
25.求函数f(x)的单调递增区间;
26.当a∈(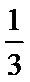
正确答案
(1)a≤0时,单调递增区间为(1,+∞);0<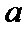
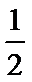
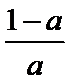
a=
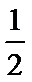
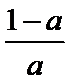
a>1时, 单调递增区间为(0,1).
解析
解:(1)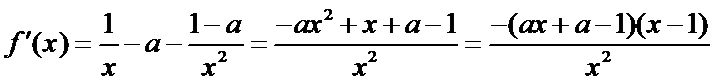
令
当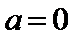
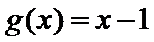
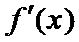
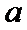
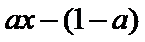
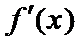
当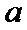
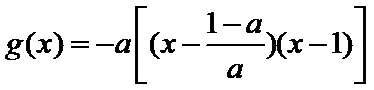
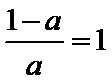
当0<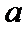
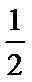
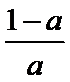
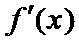
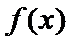
当a= 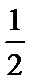
当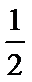
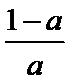
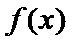
当a>1时,x∈(0,1)时,f'(x)>0,f(x)单调递增.
综上所述, a≤0时,单调递增区间为(1,+∞);
0<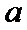
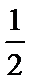
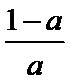
a=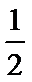
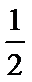
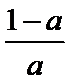
a>1时, 单调递增区间为(0,1).
考查方向
解题思路
(1)对函数进行求导,再对会影响导数符号的部分进行分类讨论;从而探索其单调性(2)由(1)对a进行分段探讨函数的单调性及在(0,t]上的最小值情况,从而确定参数的取值范围。
易错点
对参数a分类不清晰,对多个参数处理思路乱。
正确答案
(2)
解析
解:
(2)由题知函数
①当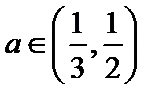
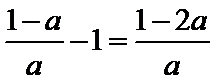
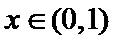
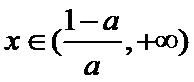
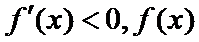
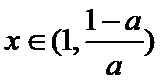
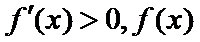
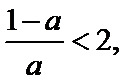
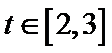
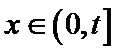
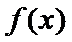
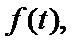
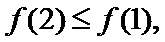
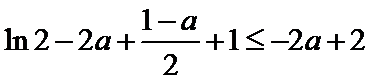
②当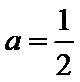
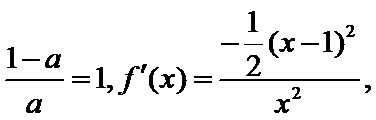
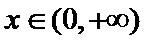
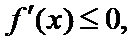
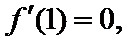
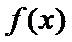
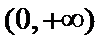
③当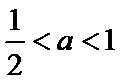
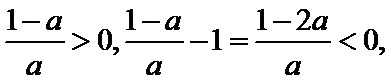
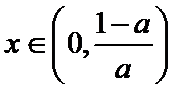
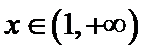
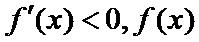
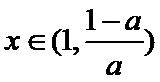
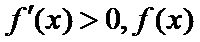
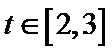
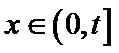
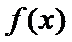
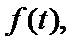
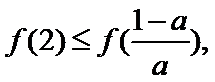
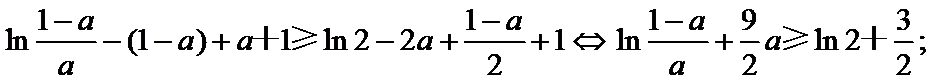
所以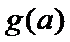
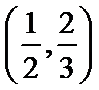
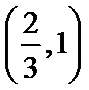
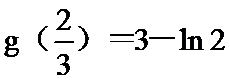
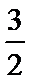
综上所述: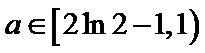
考查方向
解题思路
(1)对函数进行求导,再对会影响导数符号的部分进行分类讨论;从而探索其单调性(2)由(1)对a进行分段探讨函数的单调性及在(0,t]上的最小值情况,从而确定参数的取值范围。
易错点
对参数a分类不清晰,对多个参数处理思路乱。
已知函数

27. 讨论
28. 设曲线




29. 若关于


正确答案
(I) 当









解析
(I)解:由






下面分两种情况讨论:
(1)当
令


当


-
+
-
所以,




当


当


所以,


考查方向
解题思路
利用导数的运算、导数的几何意义解答。
易错点
不会分类讨论。
正确答案
(II)见解析;
解析
(II)证明:设点










由于















考查方向
解题思路
利用导数研究函数的性质、证明不等式等基础知识和方法.
易错点
不会利用导数的几何意义来解答。
正确答案
(III)见解析.
解析
(III)证明:不妨设








类似地,设曲线






设方程






由此可得
因为


所以,
考查方向
解题思路
分类讨论思想、函数思想和划归思想,综合分析问题和解决问题的能力。
易错点
难度大做不出来。
19.已知函数

(1)证明:当|a|≥2时,M(a,b)≥2;
(2)当a
正确答案
(1)详见解析;(2)3;
解析
试题分析:(1)分析题意可知





(1)由f(x)= 














(2)由M(a,b)








考查方向
解题思路
(1)根据a的取值范围,得到函数在[-1,1]上的单调性,分类讨论证得结论;(2)由题中给出的新定义进行求解.
易错点
二次函数在闭区间上的单调性.
知识点
已知函数
27.设
28.证明:存在




正确答案
当






解析
由已知,函数


所以
当


在区

当


解题思路
首先对函数




易错点
不会确定分类的标准导致出错或不分类;
正确答案
详见解析.
解析
由

令
则
故存在

令
由


所以
即
当

由(1)知,函数

故当


当


所以,当

综上所述,存在




考查方向
解题思路
要使得













因为










当



故当







易错点
找不到解决问题的思路导致无法入手。
已知函数f(x)=
25.若m∈(-2,2),求函数y=f(x)的单调区间;
26.若m∈(0,
正确答案
见解析
解析
解:(1)函数定义域为
①
②

③

综上所述,①
②
③
考查方向
解题思路
本题解题思路
1)借助导函数的性质,直接得出单调区间,这里特别主要零点的位置需要讨论,
2)根据第一问结论得到转换
3)构造新函数
易错点
本题易错在函数分类讨论不清,
正确答案
见解析
解析
解:
(2)当
令
①当



②当








其中
令


因


所以

使得
所以


所以
所以


所以函数f(x)的图象总在直线
考查方向
解题思路
本题解题思路
1)借助导函数的性质,直接得出单调区间,这里特别主要零点的位置需要讨论,
2)根据第一问结论得到转换
3)构造新函数
易错点
本题易错在函数分类讨论不清,
在△ABC中,角A,B,C的对边分别为


16.求角A的大小;
17.设函数

正确答案
(1)
解析
试题分析:本题属于三角函数的基本问题,题目的难度是逐渐由易到难,(1)直接按步骤来求,(2)要注意三角恒等变换的正确性;
(1)在


在△ABC中,因为

所以


考查方向
解题思路
1)第一问中利用余弦定理得到

2)第二问中用倍角公式,和差公式可得
易错点
1)第一问中用余弦定理得到


2)第二问中用倍角公式,和差公式可得
正确答案
(2)
解析
试题分析:本题属于三角函数的基本问题,题目的难度是逐渐由易到难,(1)直接按步骤来求,(2)要注意三角恒等变换的正确性;
(2)由(1)得
令
即函数
考查方向
解题思路
1)第一问中利用余弦定理得到

2)第二问中用倍角公式,和差公式可得
易错点
1)第一问中用余弦定理得到


2)第二问中用倍角公式,和差公式可得
扫码查看完整答案与解析