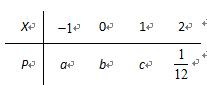- 求离散型随机变量的分布列
- 共28题
知离散型随机变量x的分布列如右表。若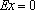
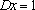
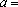
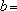
正确答案
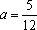
解析
由题知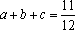
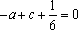
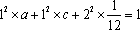
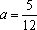
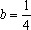
知识点
通过随机询
由
参照右上附表，得到的正确结论（ ）
A在犯错误的概率不超过
B在犯错误的概率不超过
C有
D有
正确答案
解析
略
知识点
PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物. PM2.5日均值在35微克/立方米以下空气质量为一级；在35微克/立方米
石景山古城地区2013年2月6日至15日每天的PM2.5监测数据如茎叶图所示。
（1）小陈在此期间的某天曾经来此地旅游，求当天PM2.5日均监测数据未超标的概率;
（2）小王在此期间也有两天经过此地，这两天此地PM2.5监测数据均未超标.请计算出这两天空气质量恰好有一天为一级的概率;
（3）从所给10天的数据中任意抽取三天数据，记
正确答案
见解析
解析
（1）记“当天PM2.5日均监测数据未超标”为事件A,
（2）记“这两天此地PM2.5监测数据均未超标且空气质量恰好有一天为一级” 为事件B, 
（3）
其分布列为：
知识点
某工厂生产甲、乙两种产品，甲产品的一等品率为80%，二等品率为20%；乙产品的一等品率为90%，二等品率为10%。生产1件甲产品，若是一等品则获得利润4万元，若是二等品则亏损1万元；生产1件乙产品，若是一等品则获得利润6万元，若是二等品则亏损2万元。设生产各种产品相互独立。
（1）记X（单位：万元）为生产1件甲产品和1件乙产品可获得的总利润，求X的分布列；
（2）求生产4件甲产品所获得的利润不少于10万元的概率。
正确答案
见解析。
解析
（1）由题设知，X的可能取值为10，5，2，-3，且
P（X=10）=0.8×0.9=0.72， P（X=5）=0.2×0.9=0.18，
P（X=2）=0.8×0.1=0.08， P（X=-3）=0.2×0.1=0.02。
由此得X的分布列为：
（2）设生产的4件甲产品中一等品有
由题设知
又
所求概率为
答：生产4件甲产品所获得的利润不少于10万元的概率为0.8192。
知识点
一个均匀的正四面体骰子的四个面上分别标有数字l，2，3，4，现将这颗骰子随机抛掷两次,底面上数字分别为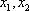 
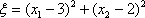
（1）分别求出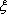 
（2）求出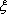
正确答案
见解析
解析
知识点
扫码查看完整答案与解析