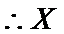- 求离散型随机变量的分布列
- 共28题
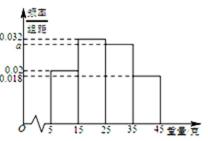
一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取
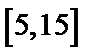
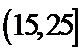
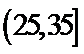
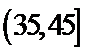
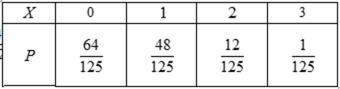
19.求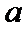
20.从盒子中随机抽取
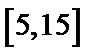

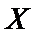
正确答案
估计盒子中小球重量的平均值约为
解析
(Ⅰ)由题意,得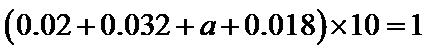
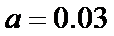
又由最高矩形中点的的横坐标为20,可估计盒子中小球重量的众数约为20(克),
而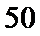
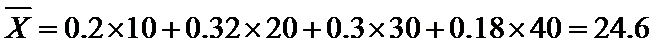
考查方向
解题思路
根据频率分布直方图求出a的值,然后根据直方图估计盒子中小球重量的众数与平均值;
易错点
不会根据频率分布直方图估计平均数;
正确答案
(2)

(或者
解析
(Ⅱ)利用样本估计总体,该盒子中小球重量在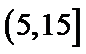
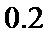
则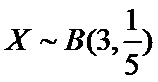

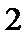
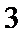
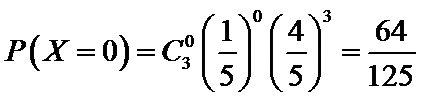
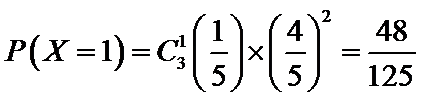
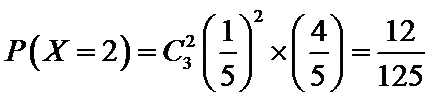
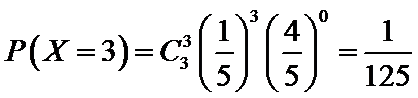

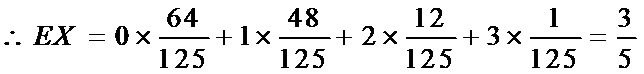
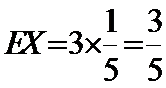
考查方向
解题思路
根据题意判断出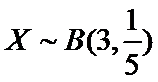
易错点
看不出二项分布导致运算很麻烦。
某市A,B两所中学的学生组队参加辩论赛,A中学推荐3名男生,2名女生,B中学推荐了3名男生,4名女生,两校推荐的学生一起参加集训,由于集训后队员的水平相当,从参加集训的男生中随机抽取3人,女生中随机抽取3人组成代表队
18.求A中学至少有1名学生入选代表队的概率.
19.某场比赛前,从代表队的6名队员中随机抽取4人参赛,设X表示参赛的男生人数,求X得分布列和数学期望.
正确答案
A中学至少1名学生入选的概率为
解析
由题意,参加集训的男女生各有6名.
参赛学生全从B中抽取(等价于A中没有学生入选代表队)的概率为
因此,A中学至少1名学生入选的概率为
考查方向
解题思路
.弄清题意后直接利用古典概率的概率公式先求对立事件的概率后即可得到答案;
易错点
对于题意理解有困难,不知道说的是什么导致没有思路。
正确答案
X的分布列为:
X的期望为
解析
根据题意,X的可能取值为1,2,3.



所以X的分布列为:
因此,X的期望为
考查方向
解题思路
直接根据超几何分布求解即可。
易错点
题中的概率错误的理解为是二项分布出错。
为了解人们对于国家新颁布的“生育
19.由以上统计数据填下面2乘2列联表,并问是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异;
20.若对年龄在[5,15),[35,45)的被调查人中各随机选取两人进行调查,记选中的4人中不支持“生育二胎”人数为ξ,求随机变量ξ的分布列及数学期望.
参考数据:
正确答案
见解析
解析
解:(Ⅰ)2乘2列联表

所以没有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异.
考查方向
解题思路
本题的解题思路
1)根据题意填写表格,并计算
2)对年龄在[5,15)进行区分和分类,写出所有可能
3)写出
易错点
本题第一问易错于计算出错。第二问基本事件空间漏或者重复出错
正确答案
见解析
解析
解:
(Ⅱ)
所以
所以
考查方向
解题思路
本题的解题思路
1)根据题意填写表格,并计算
2)对年龄在[5,15)进行区分和分类,写出所有可能
3)写出
易错点
本题第一问易错于计算出错。第二问基本事件空间漏或者重复出错
17. 一个袋中装有7个大小相同的球,其中红球有4个,编号分别为1,2,3,4;蓝球3个,编号为2,4,6,现从袋中任取3个球(假设取到任一球的可能性相同).
(

(II)记

正确答案
见解析
解析
考查方向
解题思路
本题的解题思路
1)使用排列组合知识写出基本事件空间和含有编号为2的球个数,并用古典概型的概率公式计算概率
2)分清
3)根据情况依次求概率
4)写分布列以及期望
易错点
本题易错在第一问分类不清,第二问把超几何分布当成二项分布
知识点
端午节吃粽子是我国的传统习俗,设一盘中装有10个粽子,其中豆沙粽2个,肉粽3个,白粽5个,这三种粽子的外观完全相同,从中任意选取3个。
(本小题满分13分,(1)小问5分,(2)小问8分)
17.求三种粽子各取到1个的概率;
18.设X表示取到的豆沙粽个数,求X的分布列与数学期望
正确答案

解析
试题分析:本题属于古典概型,从10个棕子中任取3个,基本事件的总数为

试题解析:(1)令A表示事件“三个粽子各取到1个”,则由古典概型的概率计算公式有

考查方向
解题思路
在解古典概型概率题时,首先把所求样本空间中基本事件的总数


易错点
,对实际的含义要正确理解.
正确答案
分布列见解析,期望为
解析
试题分析:(2)由于10个棕子中有2个豆沙棕,因此


试题解析:(2)X的所有可能取值为0,1,2,且
综上知,X的分布列为
故
考查方向
解题思路
求解一般的随机变量的期望和方差的基本方法是:先根据随机变量的意义,确定随机变量可以取哪些值,然后根据随机变量取这些值的意义求出取这些值的概率,列出分布列,根据数学期望和方差的公式计算.
易错点
注意在求离散型随机变量的分布列时不要忽视概率分布列性质的应用
扫码查看完整答案与解析