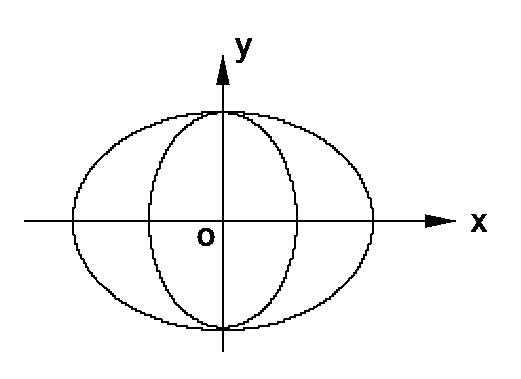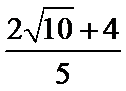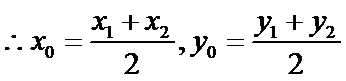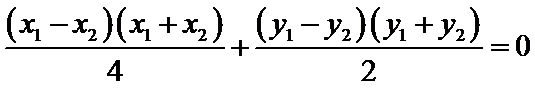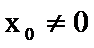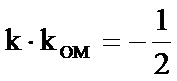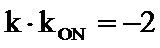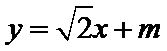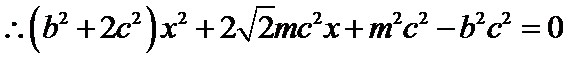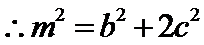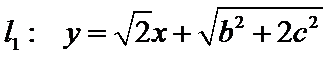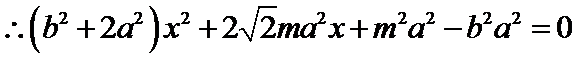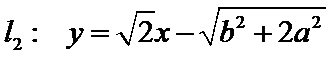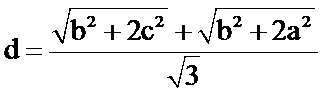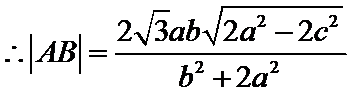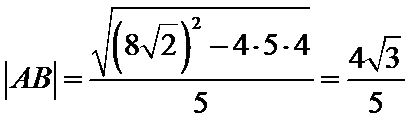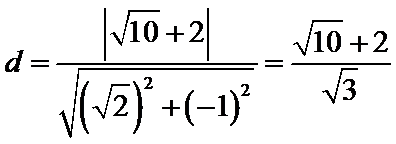- 圆锥曲线的定点、定值问题
- 共61题
21.(本题满分14分)本题共2个小题,第1小题满分6分,第2小题满分8分
双曲线





(1) 若


(2) 设



正确答案
(1)由已知
取
∵
∴
即
∴
∴渐近线方程为
(2)若
∴
设



∴

∵
∴
∴代入(*)式,可得
直线
∴
设直线

得
∴
∴
∴
∴直线
知识点
20.设圆
(I)证明
(II)设点E的轨迹为曲线C1,直线l交C1于M,N两点,过B且与l垂直的直线与圆A交于P,Q两点,求四边形MPNQ面积的取值范围.
正确答案
知识点
(本小题满分13分)
已知椭圆E:
(I)求椭圆E的方程及点T的坐标;
(II)设O是坐标原点,直线l’平行于OT,与椭圆E交于不同的两点A、B,且与直线l交于点P.证明:存在常数λ,使得∣PT∣2=λ∣PA∣·∣PB∣,并求λ的值.
正确答案
(I)由已知,

有方程组

方程①的判别式为


此方程①的解为
所以椭圆E的方程为
点T坐标为(2,1).
(II)由已知可设直线

有方程组
所以P点坐标为(

设点A,B的坐标分别为
由方程组

方程②的判别式为


由②得
所以
同理
所以

故存在常数

知识点
19.已知椭圆C:


(Ⅰ)求椭圆C的方程;
(Ⅱ)设动直线





正确答案
(Ⅰ)
(Ⅱ)

解析
试题分析:本题属于解析几何的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求,(2)要注意直线不存在斜率的特殊情况,(3)要注意计算结果去正确性
(Ⅰ)解:由题意,得

又因为点

所以
解得


所以椭圆C的方程为
(Ⅱ)结论:存在符合条件的圆,且此圆的方程为
证明如下:
假设存在符合条件的圆,并设此圆的方程为
当直线


由方程组

因为直线

所以

由方程组

则
设



设直线



所以

将

要使得


所以当圆的方程为




当直线


此时,圆



综上,当圆的方程为




考查方向
本题主要考查了椭圆的标准方程、直线与椭圆的位置关系,直线与圆锥曲线的位置关系的考查主要分以下几类:
1.直线与圆锥曲线的公共点个数问题,
2.弦长问题,
3.中点弦问题.
解题思路
本题考查直线与椭圆的位置关系,解题步骤如下:
1.利用待定系数法求出椭圆的标准方程;
2.假设存在,设出圆的方程与直线方程;
3.联立直线与椭圆的方程,化简得到关于

4.联立直线与圆的方程,化简得到关于
5.讨论直线斜率不存在的情况,得到结论。
易错点
1、第二问中,联立直线与圆的方程得到关于关于
2、第二问中,不要忘记“直线无斜率”的特殊情况。
知识点
22.如图,曲线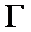
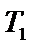
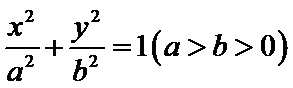
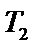
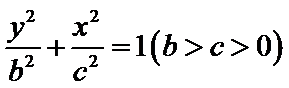
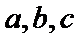
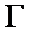
(1)
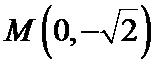
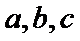
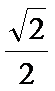
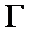
(2) 对于题(1)中的求猫眼曲线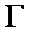
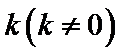
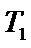
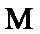
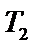

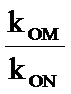
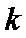
(3) 若斜率为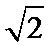
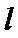
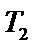
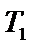
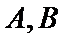
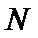
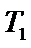
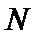
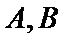
正确答案
(1) 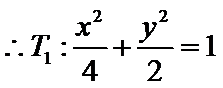
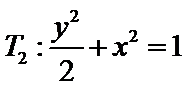
(2)证法略;
(3)
解析
(1)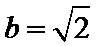
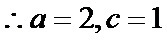
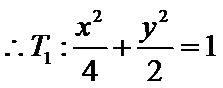
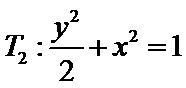
(2)设斜率为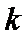
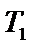
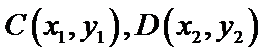
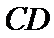
由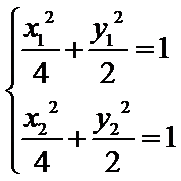
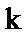

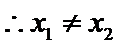
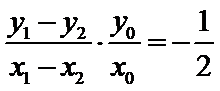
同理,
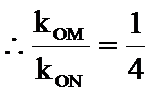
(3)设直线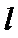
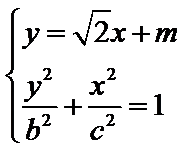
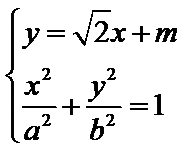
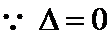
两平行线间距离:
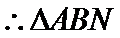
注:若用第一小题结论,算得:
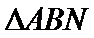
考查方向
解题思路
本题考查了椭圆的定义,方程的求法,直线与椭圆的位置关系,解题步骤如下:
(1)待定系数法求出椭圆方程;
(2)点差法推导直线的斜率的关系;
(3)利用设而不求,弦长公式求解三角形面积,
易错点
注意焦点位置的变化,区分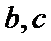
知识点
扫码查看完整答案与解析