- 函数的值域
- 共123题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
对于实数x,y,若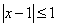
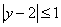
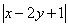
正确答案
5
解析
此题,看似很难,但其实不难,首先解出x的范围,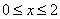
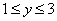
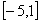
知识点
已知函数
(1)若

(2)证明:
正确答案
见解析。
解析
(1)

题设

令
当





综上,

(2)由(1)知,

当

当
所以
知识点
数列{xn}满足x1=0,xn+1=﹣x2n+xn+c(n∈N*)。
(1)证明:{xn}是从递减数列的充分必要条件是c<0;
(2)求c的取值范围,使{xn}是递增数列。
正确答案
见解析
解析
(1)当c<0时,xn+1=﹣x2n+xn+c<xn,
∴{xn}是单调递减数列充分条件
当{xn}是单调递减数列时
x1=0>x2=﹣x21+x1+c
∴c<0
综上{xn}是从递减数列的充分必要条件是c<0;
(2)由(1)得,c≥0
①当c=0时,xn=x1=0,此时数列为常数列,不符合题意;
②当c>0时,x2=c>x1=0,x3=﹣c2+2c>x2=c
∴0<c<1

⇔0=x1≤xn<

当c

由x2﹣x1=c>0⇒xn+1﹣xn>0⇔xn+1>xn。



当c

与数列{xn}是从递减数列矛盾。
所以当0<c
知识点
在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,若极坐标方程为ρcos θ=4的直线与曲线
正确答案
16
解析
由极坐标方程ρcos θ=4,化为直角坐标方程可得x=4,而由曲线参数方程消参得x3=y2,
∴y2=43=64,即y=±8,
∴|AB|=|8-(-8)|=16
知识点
设P1,P2,…,Pn为平面α内的n个点,在平面α内的所有点中,若点P到点P1,P2,…,Pn的距离之和最小,则称点P为点P1,P2,…,Pn的一个“中位点”,例如,线段AB上的任意点都是端点A,B的中位点,现有下列命题:
①若三个点A,B,C共线,C在线段AB上,则C是A,B,C的中位点;
②直角三角形斜边的中点是该直角三角形三个顶点的中位点;
③若四个点A,B,C,D共线,则它们的中位点存在且唯一;
④梯形对角线的交点是该梯形四个顶点的唯一中位点。
其中的真命题是__________。(写出所有真命题的序号)
正确答案
①④
解析
由“中位点”可知,若C在线段AB上,则线段AB上任一点都为“中位点”,C也不例外,故①正确;
对于②假设在等腰Rt△ABC中,∠ACB=90°,如图所示,点P为斜边AB中点,设腰长为2,则|PA|+|PB|+|PC|=


对于③,若B,C三等分AD,若设|AB|=|BC|=|CD|=1,则|BA|+|BC|+|BD|=4=|CA|+|CB|+|CD|,故③错;
对于④,在梯形ABCD中,对角线AC与BD的交点为O,在梯形ABCD内任取不同于点O的一点M,则在△MAC中,|MA|+|MC|>|AC|=|OA|+|OC|,
同理在△MBD中,|MB|+|MD|>|BD|=|OB|+|OD|,
则得,
|MA|+|MB|+|MC|+|MD|>|OA|+|OB|+|OC|+|OD|,
故O为梯形内唯一中位点是正确的。
知识点
设





(1)求
(2)证明

⑶证明

正确答案
见解析。
解析
知识点
设集合A={1,2,3,4,5,6},B={4,5,6,7,8},则满足

正确答案
解析
略
知识点
如图1所示,过




正确答案
6
解析
由圆的切割线定理得:



知识点
对于具有相同定义域D的函数










①



③



其中, 曲线

正确答案
解析
要透过现象看本质,存在分渐近线的充要条件是













知识点
扫码查看完整答案与解析














