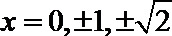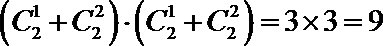- 函数的值域
- 共123题
6.某几何体的三视图如图所示,其中正（主）视图是腰长为5且底边长为8的等腰三角形,俯视图是半径为4的半圆,则该几何体的表面积是（ ）
正确答案
解析
由三视图可得,该几何体为圆锥的一半,那么该几何体的表面积为该圆锥表面积的一半与轴截面面积的和.该几何体的侧面积为
知识点
2.数列{an}中,a1=-1,a2=2,且满足an+1=an+an+2,则a2016的值为（ ）
正确答案
解析
依次求得
a3=3,
a4=1,
a5=-2,
a6=-3,
a7=-1,a8=2,
∴ {an}的周期为6,
∴ a2016=a6=-3.
知识点
12．已知函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5.儿子身高为1.30米,在地面上选取C,D两点, 儿子从C,D两点分别看我的头顶的仰角为30°,45°,且C,D两点间的距离为0.5 m,则我的高度约为（ ）.（精确到0.01米）
正确答案
解析
如图,设儿子的头顶分别为A,B两点,
在△PAB中,∠PAB=30°,
∠APB=15°,AB=0.5,
sin 15°=sin(45°-30°)=sin 45°cos 30°-cos 45°sin 30°=
由正弦定理,得
所以我的高度约为1.30+PB·sin 45°=1.30+
知识点
3.若函数y=f(x)的值域是[2,3],则函数
A
B
C
D
正确答案
解析
令t=f(x),则t∈[2,3],
则
可化为
因为
所以函数y在[2,3]上递增,所以
故函数F(x)的值域为
故选C.
知识点
8.已知向量a=（sin x,
正确答案
解析
f(x)=2(a+b)·b=
所以f(x)+4cos(2A+
因为x∈[0,
所以
知识点
4.若直线
A
B1
C
D
正确答案
解析
设向量m=(cos α,sin α),
由题意知
可得1=
即
故选B.
知识点
9.已知点P(x,y)是椭圆
正确答案
解析
根据题意,令
因此
所以当
x-y取最小值
知识点
2．函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．已知函数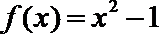
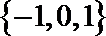
正确答案
9
解析
∵函数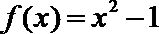
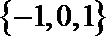
由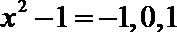
∴函数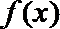
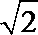
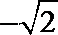
∴函数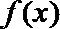
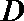
共9种可能，故这样的集合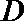
考查方向
本题主要考查函数的概念及其构成元素、排列组合的知识，考查学生分析问题的能力，是容易题．
解题思路
由题意知，函数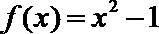
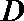
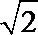
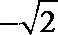
易错点
再求得定义域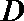
知识点
扫码查看完整答案与解析