函数的值域_章节学习

1

题型：单选题

|

单选题 · 5 分

8.已知实数.( )

A若则

B若则

C若则

D若则

正确答案

D

解析

A.令，排除此选项，B.令排除此选项，C.令排除此选项，故选D，

考查方向

含参数的绝对值不等式的性质

解题思路

举反例排除法

易错点

逐个去证明，方法不可取。

知识点

函数的值域

1

题型：填空题

|

填空题 · 12 分

（本小题满分12分）

(I)讨论函数的单调性，并证明当 >0时，

(II)证明：当时，函数有最小值.设g（x）的最小值为，求函数的值域.

正确答案

（Ⅰ）的定义域为.

且仅当时，，所以在单调递增，

因此当时，

所以

（II）

由（I）知，单调递增，对任意

因此，存在唯一使得即，

当时，单调递减；

当时，单调递增.

因此在处取得最小值，最小值为

于是，由单调递增

所以，由得

因为单调递增，对任意存在唯一的

使得所以的值域是

综上，当时，有，的值域是

知识点

函数的值域函数单调性的判断与证明函数的最值及其几何意义导数的运算

1

题型：单选题

|

单选题 · 5 分

16．已知点的坐标为，将绕坐标原点逆时针旋转至，则点的纵坐标为（）

A

B

C

D

正确答案

D

解析

，即点的纵坐标为.

考查方向

本题主要考查三角函数值的计算，根据三角函数的定义以及两角和差的正弦公式是解决本题的关键

解题思路

根据三角函数的定义，求出∠xOA的三角函数值，利用两角和差的正弦公式进行求解即可．

易错点

旋转前后的坐标问题

知识点

函数的值域

1

题型：简答题

|

简答题 · 12 分

设函数。

26.讨论的导函数零点的个数；

27.证明：当时，。

第(1)小题正确答案及相关解析

正确答案

第(2)小题正确答案及相关解析

正确答案

1

题型：单选题

|

单选题 · 5 分

9.已知函数f(x)的定义域为R.当x<0时，；当时，；当时， .则f(6)=

A−2

B−1

C0

D2

正确答案

D

解析

当时，,所以当时，函数是周期为的周期函数，所以，又因为函数是奇函数，所以，故选D.

考查方向

本题考查了函数的周期性、奇偶性，灵活变换求得函数性质是解题的关键，难度中等.

解题思路

先通过求出函数周期1,将函数中的自变量化小,然后结合奇函数性质求值.

易错点

【易错点】满足：f(x＋a)＝f(x－a)，f(x＋a)＝-f(x)；的函数都是周期函数, 且Ｔ＝2a.

知识点

函数的值域

1

题型：填空题

|

填空题 · 5 分

14．设a＝，则二项式展开式中含项的系数是________．

正确答案

-192

解析

a＝=，，若某一项含有，则，该项的系数为，故答案为-192.

考查方向

本题主要考查了定积分的运算、二项式定理及其通项公式。定积分是新课程增加的内容，二项式定理是高考的热点考题，两部分内容均需要高度重视。

解题思路

先求出a，然后再确定含的项，最后即可求解。

易错点

对二项展开式的通项公式应用不熟练而导致错误的出现。

知识点

函数的值域

1

题型：单选题

|

单选题 · 5 分

2．下列函数中，值域为的偶函数是（）

A

B

C

D

正确答案

C

解析

因为的值域为，所以排除选项A；因为，即是奇函数，所以排除选项B；因为的值域为，所以排除选项D；因为的值域为，且，即为偶函数，所以选C选项。

考查方向

本题主要考查了函数的值域和函数的奇偶性。

解题思路

通过逐一验证函数的值域和奇偶性进行排除得到答案。

易错点

本题易在判定选项D的值域时出现错误，易忽视，而不是。

知识点

函数的值域函数奇偶性的判断

1

题型：单选题

|

单选题 · 5 分

12.若函数在上的值域为，则称函数为“和谐函数”.

下列函数中：

①；

②；

③；

④，“和谐函数”的个数为（）

A1个

B2个

C3个

D4个

正确答案

C

解析

试题分析：由题意知，若在区间上单调递增，须满足：，，结合图象知：①④正确，③错误；若在区间上单调递减，须满足：，，对于②，代入有，即可，例如：满足题意，所以②正确，故选C．

考查方向

本题主要考查了新定义、函数的单调性、函数的图象等知识点，为高考必考题，在近几年的各省高考题出现的频率较高，常与几函数的图像及、性质等知识点交汇命题。

易错点

不能由三视图还原为原图导致出错。

知识点

函数的定义域及其求法函数的值域

1

题型：单选题

|

单选题 · 5 分

12.函数.给出函数下列性质：

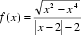
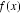
①函数的定义域和值域均为；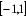

②函数的图像关于原点成中心对称；

③函数在定义域上单调递增；

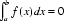
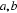
④（其中为函数在定义域上的积分下限和上限）；

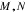
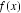
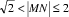
⑤为函数图象上任意不同两点，则.

则关于函数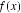性质正确描述的序号为（）

A①②⑤

B①③⑤

C②③④

D②④

正确答案

D

解析

根据已知解析式可知，

函数，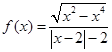

因为-1 ，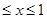

那么原式化简为，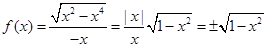

然后分析函数的定义域和值域均为，错误。

函数是奇函数，可知关于原点成中心对称，

同时在定义域内递增，并且命题4，利用对称性可知定积分值为零，

命题5中，不成立，故正确的序号为②④。

A选项不正确，B选项不正确，C选项不正确，所以选D选项。

考查方向

本题主要考查函数的性质

解题思路

1、化简函数解析式；

2、依次判断每个命题，即可得到结果。

A选项不正确，B选项不正确，C选项不正确，所以选D选项。

易错点

本题易在判断化简时发生错误。

知识点

命题的真假判断与应用函数的定义域及其求法函数的值域奇偶函数图象的对称性

1

题型：单选题

|

单选题 · 5 分

2. 下列函数中，值域为的偶函数是（）

A

B

C

D

正确答案

C

解析

由（A）的值域为 B 值域为Ｒ（D）函数的值域都不是从而排除Ａ、Ｂ、Ｄ，选择Ｃ答案。

考查方向

本题主要考查了函数值域的求法及偶函数的概念和判断方法

解题思路

先由函数的值域为而排除不符合题意的选项，再判断其奇偶性从而确定正确答案。

易错点

不会求值域或不会判断偶函数而出错

知识点

函数的值域函数奇偶性的判断

热门试卷

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

正确答案

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点