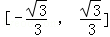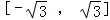函数的值域
共123题

· 函数的值域

函数的值域
共123题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

已知函数的图象与直线的三个相邻交点的横坐标分别是，则的单调递增区间是

D无法确定

正确答案

解析

略

知识点

函数的值域

题型：简答题

简答题 · 14 分

已知函数的图象为曲线, 函数的图象为直线.

（1）当时, 求的最大值;

（2）设直线与曲线的交点的横坐标分别为 , 且 ,求证: .

正确答案

见解析

解析

解析：（1）

单调递增，单调递减，

（2）不妨设，要证

只需证

即证，

即 .即

令,即证

φ(t)在（1，﹢∞）单调递增， ∵φφ(1)=0 ∴φ(t)>0

即

∴

知识点

函数的值域

题型：简答题

简答题 · 14 分

在△ABC中，角A，B，C所对的边分别为a，b，c，已知，且。

（1）求角A，B的大小；

（2）设函数，求函数的周期及其在[，]上的值域。

正确答案

见解析

解析

（1）∵，由正弦定理得，即

∴或（舍去），，则

（2）

∵，则

而正弦函数在上单调递增，在上单调递减

∴函数的最小值为，最大值为，

即函数在上的值域为。

知识点

函数的值域

题型：简答题

简答题 · 12 分

平面直角坐标系xOy中，椭圆C：，椭圆上、下顶点分别为B1，B2，椭圆上关于原点对称两点M（m,n），N（—m,—n）和椭圆上异于M，N两点的任一点P满足直线PM，PN的斜率之积等于—（直线PM，PN都不垂直于x轴），焦点F（c,0）在直线上，直线y=kx+2与椭圆交于不同两点S，T。

（1）求C的方程；

（2）求证：直线B1S与直线B2T的交点在一条定直线上，并求出这条定直线。

正确答案

见解析

解析

（1）设椭圆上点且点在椭圆上

做差得

又在直线上，令，得，

所以椭圆方程为

（2）

取直线与椭圆交于两点

直线，两条直线的交点为

取直线与椭圆交于两点

直线，两条直线的交点为

若交点在一条直线上则此直线只能为

验证对任意的，直线与直线的交点都在定直线上，设直线直线与直线交点为，直线与直线交点为，设点

直线

；

所以点与重合，所以交点在直线上

知识点

函数的值域

题型：单选题

单选题 · 5 分

的值域是（　　）

B [﹣1，1]

C[﹣2，2]

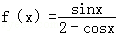
正确答案

解析

解：∵，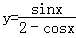

∴1+sinx=2y+ycosx，

∴sinx+ycosx=2y，

即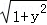：sin（x+θ）=2y，

∵|sin（x+θ）|≤1，

∴﹣≤2y≤，

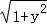
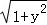
解得：y∈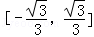，故选：A。

知识点

函数的值域两角和与差的正弦函数三角函数的最值

继续学习学习下一知识点

下一知识点 : 函数的图象与图象变化

百度题库 > 高考 > 理科数学 > 函数的值域

扫码查看完整答案与解析