- 函数的值域
- 共123题
设集合A为函数y =ln(-x2-2x+8)的定义域,集合B为函数
y=x+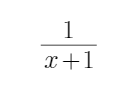
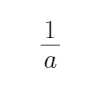
(1)求A∩B; (2)若
正确答案
见解析
解析
(1)由-x2-2x+8>0,解得A=(-4,2),又y=x+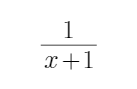
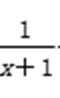
所以B=(-∞,-3]∪ [1,+∞),所以A∩B=(-4,-3]∪[1,2),
(2)因为∁RA=(-∞,-4]∪[2,+∞)。
由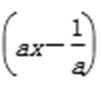
① 当a>0时,由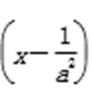

② 当a<0时,由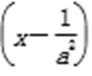
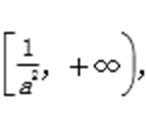
欲使C⊆∁RA,则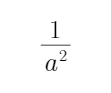
解得-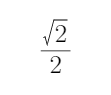
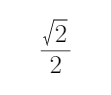
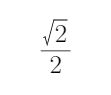
综上所述,所求a的取值范围是
知识点
已知函数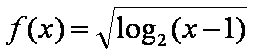
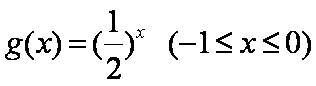
(1)求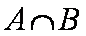
(2)若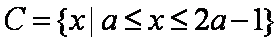
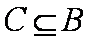
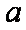
正确答案
见解析
解析
(1)由题意得: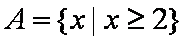
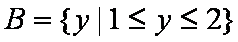
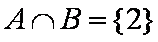
(2)由(1)知: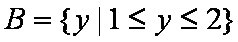
①当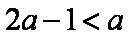
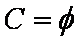
②当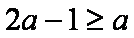
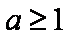
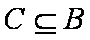

解得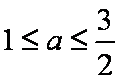
综上,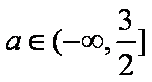
知识点
若函数f(x)=x2+ax+2b在区间(0,1)(1,2)内各有一个零点,则a2+(b﹣2)2范围( )
正确答案
解析
解:∵函数f(x)=x2+ax+2b在区间(0,1)(1,2)内各有一个零点,
∴

作出不等式组对应的平面区域如图:(阴影部分),
设P(0,2),则a2+(b﹣2)2的几何意义表示为阴影部分内的动点到定点P距离的平方。
由图象可知当AP的距离最大,CP的距离最小。
由


|CP|=
∴|AP|2=10,|CP|2=5,
即5<a2+(b﹣2)2<10,
故选B。
知识点
已知函数
(1)求
(2)若不等式

(3)数列




正确答案
见解析
解析
本题主要考查函数与导数,函数图象与性质,数列等基础知识;考查学生抽象概括能力,推理论证能力,创新能力;考查函数与方程思想,有限与无限思想,分类与整合思想,
(1) 


所以切线方程为

(2)(法一)
当



显然当


当








所以不等式


(法二)


令

当


当




所以不等式


(3) 



由(2)知,当





……

令
则



知识点
2.复数

正确答案
解析
∵复数z=1﹣i,∴





知识点
扫码查看完整答案与解析