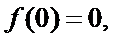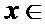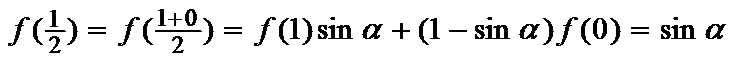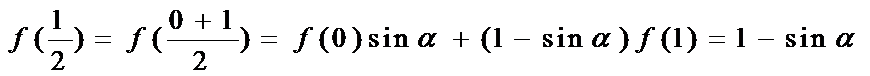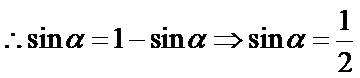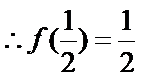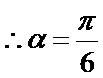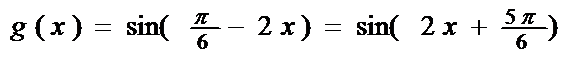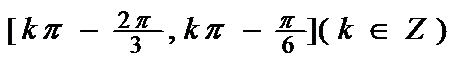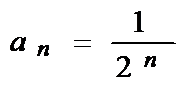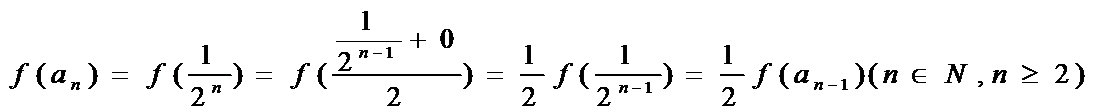- 函数的值域
- 共123题
12.若定义运算


正确答案
(0,1]
解析
解析已在路上飞奔,马上就到!
知识点
17.函数










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.已知点集






(1)求数列
(2)若




(3)若



使得

正确答案
(1)y=






所以

因为


(2)设


即


(A)当
=


(B)当
= 

而



(3)假设

(A)
(一)



则


(二)



则


(B)
(一)



则


(二)



则


由此得:对于给定常数m(





解析
解析已在路上飞奔,马上就到!
知识点
18.如图,是某市1000户居民月平均用电量的频率分布直方图,

(1)如果当地政府希望
(2)计算这1000户居民月用电量的平均值(同一组中的数据用该组区间的中点值作代表);
(3)有关部门为了制定居民月用电量标准,采用分层抽样的方法从1000户居民中抽取50户参加听证会,并且要在这已经确定的50人中随机确定两人做中心发言,求这两人分别来自用电量区间

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设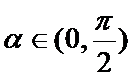
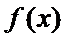
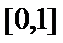
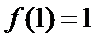
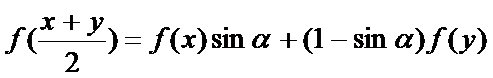
(1)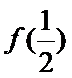
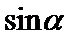
(2)函数
(3)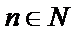
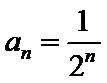

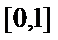
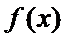
正确答案
(1)
又:
(2)由(1)知: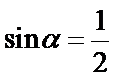
又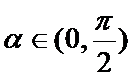
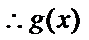
(3)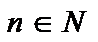
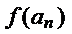
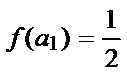
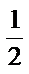
故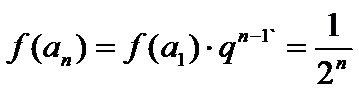
解析
解析已在路上飞奔,马上就到!
知识点
15.已知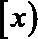

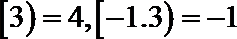
下列命题:
①函数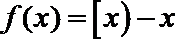
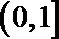
②若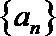
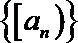
③若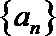
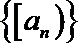
④若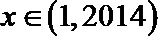
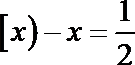
其中正确的的序号是____________.(把你认为正确的序号都填上)
正确答案
①④
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.直线l经过抛物线y2=4(x–1)的焦点,且与准线的夹角为30o,则l的方程为____.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.在边长为5的菱形ABCD中,AC=8.现沿对角线BD把△ABD折起,折起后使∠ADC的余弦值为.
(1)求证:平面ABD⊥平面CBD;
(2)若M是AB的中点,求折起后AC与平面MCD所成角的正弦值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析