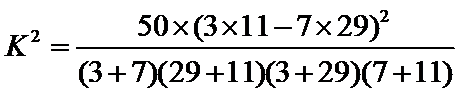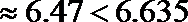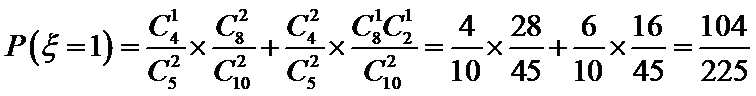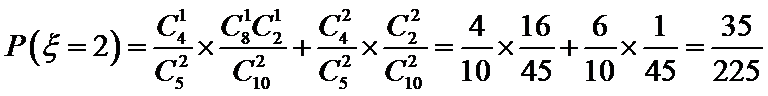- 指数函数的图像变换
- 共416题
17.设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.直线
正确答案
—15
解析
解析已在路上飞奔,马上就到!
知识点
18.现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对 “楼市限购令”赞成人数如下表.
(Ⅰ)由以上统计数据填下面2乘2列联表并问是否有99%的把握认为“月收入以5500为分界点对“楼市限购令” 的态度有差异;
(Ⅱ)若对月收入在[15,25) ,[25,35)的被调查人中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为 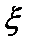
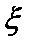
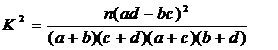
正确答案
(I)先列出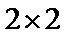
然后利用公式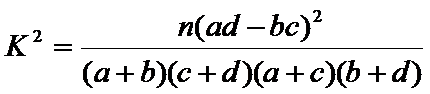
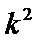
(II)先确定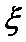
(Ⅰ)2乘2列联表
所以没有99%的把握认为月收入以5500为分界点对“楼市限购令”的态度有差异.
(Ⅱ)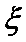
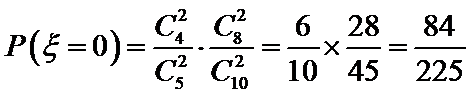
所以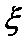
所以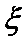
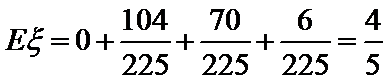
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)当


(2)如果函数












正确答案
(1)当


对于


∴

(2)在区间(1,+∞)上,函数

则
令

且


∵
1) 若



当



此时

并且在该区间上有

当


有

2) 若


从而
要使

所以
又因为h/(x)= –x+2a–

h(x)在(1, +∞)上为减函数,
h(x)<h(1)= 

所以a



解析
解析已在路上飞奔,马上就到!
知识点
12.在平面直角坐标平面上,





正确答案
2/5
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析