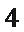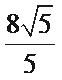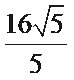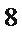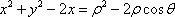- 坐标系与参数方程
- 共275题
5.直线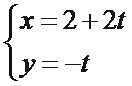
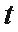
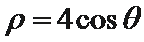
正确答案
解析
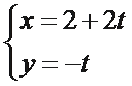
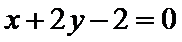
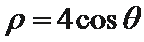
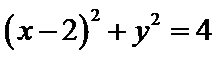
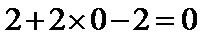
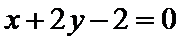
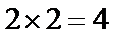
考查方向
解题思路
1.先将直线的参数方程化为普通方程,后利用极坐标与直角坐标互化公式求出其极坐标方程;2.然后发现直线经过圆心,所以求出其弦长为直径。
易错点
1.方程间的相互转化出错;2.注意不到直线经过圆的圆心的条件导致运算麻烦。
知识点
15.已知直线l的参数方程为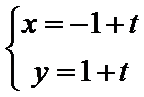
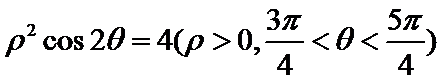
正确答案
解析
直线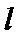
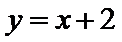
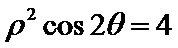
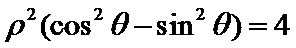
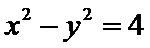
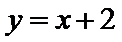
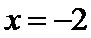
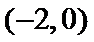
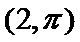
考查方向
解题思路
参数方程主要通过代入法或者已知恒等式(如
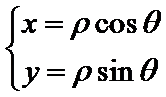
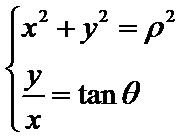
易错点
参数方程与普通方程的转化
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
在极坐标系中,圆
正确答案
解析
略
知识点
在极坐标系(ρ,θ)(0≤θ<2π)中,直线
正确答案
解析
知识点
曲线C的直角坐标方程为x2+y2-2x=0,以原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为__________。
正确答案
ρ=2cos θ
解析
本题考查极坐标方程与直角坐标方程的互化及转化与化归的数学思想.
由极坐标方程与直角坐标方程的互化公式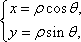
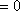
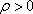
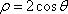
知识点
在极坐标系中,点

正确答案
解析
略
知识点
在极坐标系中,已知圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,求实数a的值。
正确答案

解析


直线3ρcosθ+4ρsinθ+a=0的普通方程为:
又圆与直线相切,所以


知识点
在极坐标系中,O为极点,直线l过圆C:
正确答案
解析
把
圆心C的坐标为(1,1),
与直线OC垂直的直线方程为x+y﹣2=0,
化为极坐标系的方程为ρcosθ+ρsinθ﹣2=0或
故答案为: ρcosθ+ρsinθ﹣2=0或
知识点
在直角坐标系







正确答案
解析
略
知识点
扫码查看完整答案与解析