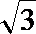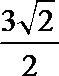- 坐标系与参数方程
- 共275题
10. 若P是极坐标方程为



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 在极坐标系中,点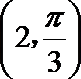
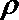
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.在直角坐标系中,曲线C:
(1)将直线l的极坐标方程化为直角坐标方程;
(2)设点P在曲线C上,求P点到直线l的距离的最大值.
正确答案
(1)直线的直角坐标方程为4x-3y-12=0
(2)当cos(
解析
解析已在路上飞奔,马上就到!
知识点
2.原点与极点重合,

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.选修4-4:坐标系与参数方程
在极坐标系中,已知圆C的圆心
(1)求圆C的极坐标方程;
(2)若点Q在圆C上运动,P在OQ的延长线上,且|OQ|∶|QP|=3∶2,求动点P的轨迹方程.
正确答案
(1)
(2)
解析
试题分析:本题属于坐标系与参数方程中的基本问题,题目的难度一般,解题过程如下:
(1)设



∵


∴


(2)设点










考查方向
解题思路
本题考查极坐标方程的知识,可以根据求圆的极坐标方程所需的条件寻求关系。
易错点
没有准确理解极坐标下的轨迹方程而导致本题不会做。
知识点
已知抛物线





正确答案
解析
将

知识点
在极坐标系中,圆


(1)求圆C的标准方程和直线
(2)若直线

正确答案
见解析
解析
(1)由
所以直线

由
又
所以,圆

(2)因为直线


两边平方得
所以a的取值范围是
知识点
已知圆





(1)将圆

(2)圆

正确答案
见解析
解析
解析:(1)由
又∵ρ=2cos(θ+)=cosθ-sinθ,
∴ρ2=ρcosθ-ρsinθ.
∴x2+y2-x+y=0,即
(2)圆心距
由得,A(1,0),B
∴ 
知识点
选做题:14~16题,考生只能从中选做两题
14.(坐标系与参数方程)
在极坐标系中,定点A(2,π),动点B在直线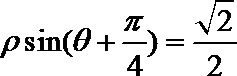
15.(几何证明选讲)
如图,在半径为2的⊙O中,∠AOB=90°,D为OB的中点,AD的延长线交⊙O于点E,则线段DE的长为____________.
16.(优选法选讲)
用0.618法选取试点的过程中,如果实验区间为[2,4],前两个试点依次为x1,x2,若x1处的实验结果好,则第三试点的值为__________.
正确答案
14.
15. 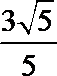
16. 3.528或2.472(填一个即可)
解析
解析已在路上飞奔,马上就到!
知识点
13.曲线


正确答案


解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析