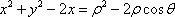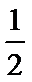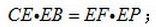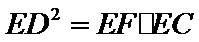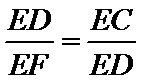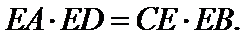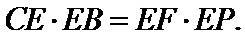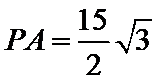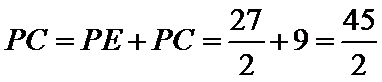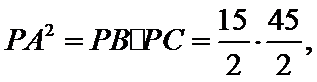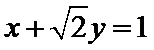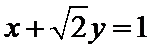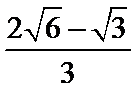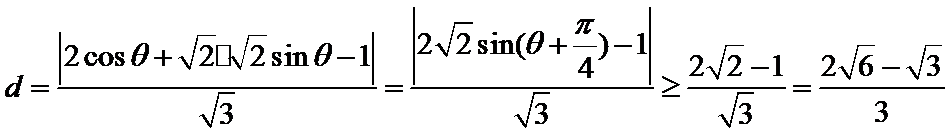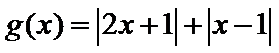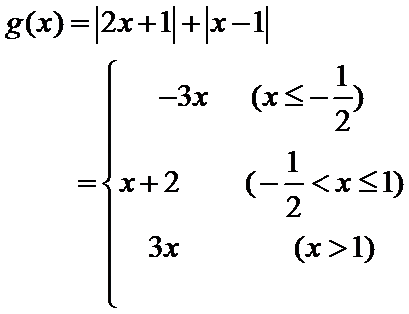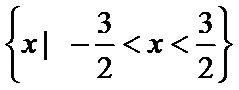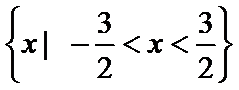- 坐标系与参数方程
- 共275题
11.在极坐标系中,直线


正确答案
2
知识点
21.选做题:在A、B、C、D四小题中只能选做2题。解答应写出文字说明、证明过程或演算步骤。
B.(选修4-2:矩阵与变换)
二阶矩阵M有特征值λ=8,其对应的一个特征向量

C.(选修4-4:坐标系与参数方程)
已知极坐标系的极点在直角坐标系的原点,极轴与x轴的正半轴重合,曲线C的极坐标系为




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
在极坐标系中,点
正确答案
1
解析
在极坐标系中,点

知识点
曲线C的直角坐标方程为x2+y2-2x=0,以原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为__________。
正确答案
ρ=2cos θ
解析
本题考查极坐标方程与直角坐标方程的互化及转化与化归的数学思想.
由极坐标方程与直角坐标方程的互化公式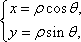
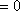
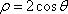
知识点
若曲线的极坐标方程为
正确答案

解析
做坐标系与参数方程的题,大家只需记住两点:1、


所以解析式为:
知识点
在极坐标系中,已知圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,求实数a的值。
正确答案

解析


直线3ρcosθ+4ρsinθ+a=0的普通方程为:
又圆与直线相切,所以


知识点
在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,圆C1,直线C2的极坐标方程分别为ρ=4sin θ,
(1)求C1与C2交点的极坐标;
(2)设P为C1的圆心,Q为C1与C2交点连线的中点,已知直线PQ的参数方程为
正确答案
(1) 

解析
(1)圆C1的直角坐标方程为x2+(y-2)2=4,
直线C2的直角坐标方程为x+y-4=0.
解
所以C1与C2交点的极坐标为

注:极坐标系下点的表示不唯一。
(2)(1)可得,P点与Q点的直角坐标分别为(0,2),(1,3)。
故直线PQ的直角坐标方程为x-y+2=0.
由参数方程可得
所以
解得a=-1,b=2
知识点
请考生在以下三题中任选一题作答,如果多做,则按所做的第一题记分.作答时用2B铅笔在答题卡上把所选题目对应的题号涂黑.
【选修4—1】几何证明选讲(请回答28、29、30题)
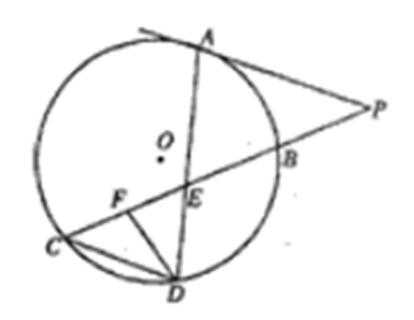
如图:已知PA切圆O于A,PBC是割线,弦CD∥AP,AD交BC于E,F在CE上,且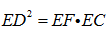
【选修4—4】坐标系与参数方程(请回答31、32题)
在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系。已知曲线C1的极坐标方程为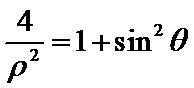
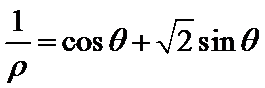
【选修4—5】不等式选讲(请回答33、34题)
已知函数
28.求证:∠EDF=∠P;
29.求证:
30.若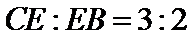
31.写出曲线C1与直线l的直角坐标方程;
32.设Q为曲线C1上一动点,求Q点到直线l距离的最小值。
33.求a的值;
34.解不等式:
正确答案
证明:∵
∴
又∵∠DEF=∠CED
∴△DEF∽△CED
∴∠C=∠EDF 又CD∥AP,
∴∠C=∠P.
∴∠EDF=∠P.
解析
证明:∵
∴
又∵∠DEF=∠CED
∴△DEF∽△CED
∴∠C=∠EDF 又CD∥AP,
∴∠C=∠P.
∴∠EDF=∠P.
考查方向
解题思路
先证明△DEF∽△CED,再根据平行求出∠EDF=∠P.
易错点
切割线定理在应用的时候出错,线段成比例找不对容易出错,相似三角形不写成对应的容易导致比例线段出错。
正确答案
证明:
由(1)得∠EDF=∠P,又∠FED=∠PEA,
∴△FED∽△AEP. ∴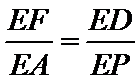
∴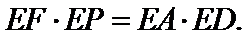
∴
解析
证明:
由(1)得∠EDF=∠P,又∠FED=∠PEA,
∴△FED∽△AEP. ∴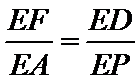
∴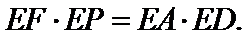
∴
考查方向
解题思路
借助第一问,求得△FED∽△AEP,进而得出成比例线段。
易错点
切割线定理在应用的时候出错,线段成比例找不对容易出错,相似三角形不写成对应的容易导致比例线段出错。
正确答案
解析
证明:
设CE=3k,EB=2k.
∵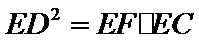
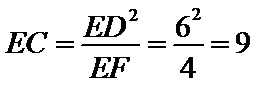
又CE=3k=9, k=3,EB=2k=6.
由(2)得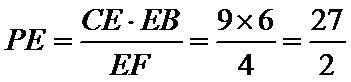
故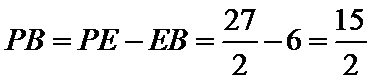
∵
∴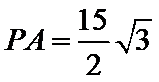
考查方向
解题思路
借助第一二问,根据成比例线段得出结果。
易错点
切割线定理在应用的时候出错,线段成比例找不对容易出错
正确答案
C1的直角坐标方程: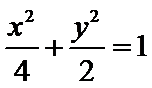
解析
根据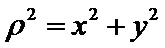
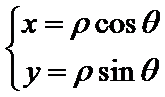
C1的直角坐标方程: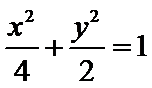
考查方向
解题思路
根据极坐标与直角坐标互化的公式可以直接得到曲线C1与直线l的直角坐标方程;
易错点
极坐标与直角坐标的转化
正确答案
解析
由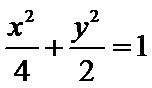
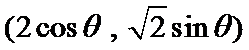
∴点Q到直线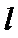
考查方向
解题思路
将曲线C1的直角坐标方程转化为参数方程,代入点Q到直线的距离公式,利用三角恒等变换得到最值。
易错点
点到直线距离公式的应用,计算出错。
正确答案
a=1
解析
可以先不考虑参数a,令
画出图形,即可知道函数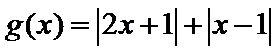
因为函数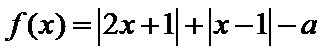
所以a=1
【三级考点】不等式的基本性质,绝对值不等式的解法
考查方向
解题思路
利用零点分段法解绝对值不等式,讨论三种情况。
易错点
在对函数的最小值进行求解时,参数的处理容易出错
正确答案
解析
把a=1代入
利用零点分段法可以得到此不等式的解集是
考查方向
解题思路
利用零点分段法解绝对值不等式,讨论三种情况。
易错点
解决第二问的时候,要注意不等式的最小值。
扫码查看完整答案与解析