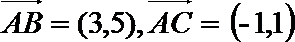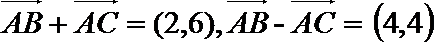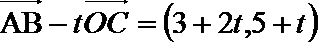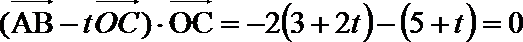平面向量数量积的运算
共301题

· 平面向量数量积的运算

平面向量数量积的运算
共301题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

15．对任意两个非零的平面向量和,定义,若平面向量、满足,与的夹角,且和都在集合中．给出下列命题：

①若时，则,

②若时，则,

③若时，则的取值个数最多为7,

④若时，则的取值个数最多为．

其中正确的命题序号是（把所有正确命题的序号都填上）

正确答案

①③

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用平面向量数量积的运算

题型：简答题

简答题 · 12 分

21． ABC中，a、b、c分别是角A、B、C的对边，＜C＜，且．

（1）判断△ABC的形状；

（2）若，求的取值范围。

正确答案

（1）

⇒sinBsinA﹣sinBsin2C=sinAsin2C﹣sinBsin2C

⇒sinB=sin2C，

因为，

所以B=π﹣2C⇒B+C=π﹣C⇒π﹣A=π﹣C⇒A=C

即△ABC为等腰三角形．

（2）因为

所以，

而

所以

解析

解析已在路上飞奔，马上就到！

知识点

三角函数中的恒等变换应用正弦定理余弦定理平面向量数量积的运算

题型：简答题

简答题 · 10 分

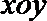
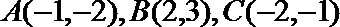
17．在平面直角坐标系中,.

（1）求以线段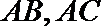为邻边的平行四边形的两条对角线的长;

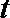
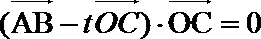
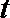
（2）设实数满足,求的值。

正确答案

（1）因为

则

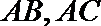
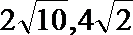
以线段为邻边的平行四边形的两条对角线的长分别为.

（2）因为

所以

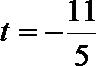
解析

解析已在路上飞奔，马上就到！

知识点

向量的模向量的加法及其几何意义向量的减法及其几何意义平面向量数量积的运算量积判断两个平面向量的垂直关系

题型：简答题

简答题 · 13 分

20.已知以原点O为中心的椭圆，它的短轴长为，右焦点(c>0)，它的长轴长为2a(a>c>0)，直线与x轴相交于点A，，过点A的直线与椭圆相交于P.Q两点。

（Ⅰ）求椭圆的方程和离心率；

（Ⅱ）若，求直线PQ的方程；

（Ⅲ）设，过点P且平行于直线的直线与椭圆相交于另一点M，证明：。

正确答案

(Ⅰ)解：由题意，可知椭圆的方程为.

由已知得

解得，c=2，

所以椭圆的方程为，离心率.

(Ⅱ)解：由（1）可得A(3，0)．设直线PQ的方程为y=k(x－3).

联立方程组，得(3k2+1)x2－18k2x+27k2－6=0，

依题意△=12(2－3k2)>0，得.

设P(x1，y1)，Q(x2，y2)，则

， ①

． ②

由直线PQ的方程得为y1=k(x1－3)，y2=k(x2－3)，于是，

y1y2=k2(x1－3) (x2－3)= k2[x1x2－3(x1+ x2)+9]. ③

∵，∴x1x2+y1y2=0． ④

由①②③④得5k2=1，从而．

所以直线PQ的方程为或．

(理科做)

(Ⅲ)证明：∵P(x1，y1)，Q(x2，y2)， A(3，0)，

∴，．由已知得方程组

，注意λ>1，解得，

因为F(2，0)， M(x1，－y1)，故

而，所以.

解析

解析已在路上飞奔，马上就到！

知识点

平面向量数量积的运算量积判断两个平面向量的垂直关系椭圆的定义及标准方程椭圆的几何性质直线、圆及圆锥曲线的交汇问题

题型：单选题

单选题 · 5 分

4．如图，在四边形中，，已知的夹角为，，则=（）

D10

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

向量的模平面向量数量积的运算数量积表示两个向量的夹角向量在几何中的应用

题型：填空题

填空题 · 5 分

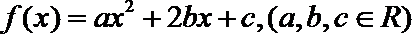
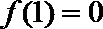
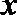
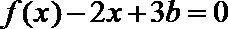
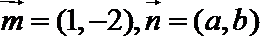
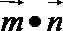
14．已知开口向上的二次函数满足，且关于的方程的两个实数根分别在区间（0，1）和（1，2）内。若向量，则的取值范围为.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的图象和性质二次函数的零点问题平面向量数量积的运算

题型：简答题

简答题 · 13 分

20．已知椭圆C: 的离心率为，以原点为圆心，椭圆C的短半轴长为半径的圆与直线相切．

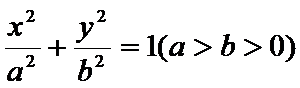
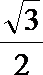
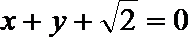
（1）求椭圆C的方程；

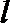
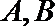
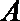
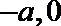
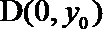
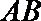
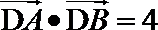
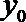
（2）设斜率不为零的直线与椭圆相交于不同的两点，已知点的坐标为（），点在线段的垂直平分线上，且，求的值。

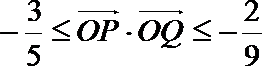
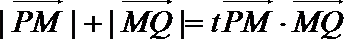
（3）若过点M(1,0)的直线与椭圆C相交于P, Q两点，如果 (O为坐标原点)，且满足，求实数t的取值范围．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面向量数量积的运算向量在几何中的应用椭圆的定义及标准方程圆锥曲线中的范围、最值问题直线、圆及圆锥曲线的交汇问题

题型：单选题

单选题 · 5 分

9．定义平面向量之间的一种运算“⊙”如下：对任意向量ab令a⊙b，则下列说法错误的是（）

A对任意的a⊙ba⊙(b)

Ba⊙bb⊙a

Ca⊙babab

D若a与b共线，则a⊙b

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用平面向量数量积的运算

题型：单选题

单选题 · 5 分

4．在中，“”是“是钝角三角形”的（）

A充分不必要条件

B必要不充分条件

C充要条件

D既不充分也不必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

充要条件的判定平面向量数量积的运算数量积表示两个向量的夹角

题型：简答题

简答题 · 12 分

17．设O为坐标原点，已知向量、分别对应复数、，，是实数，求的值。

正确答案

由

又分母不为零，

解析

解析已在路上飞奔，马上就到！

知识点

向量的模平面向量数量积的运算复数的基本概念复数代数形式的混合运算

继续学习学习下一知识点

下一知识点 : 数量积表示两个向量的夹角

百度题库 > 高考 > 理科数学 > 平面向量数量积的运算

扫码查看完整答案与解析