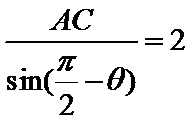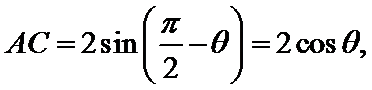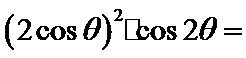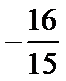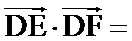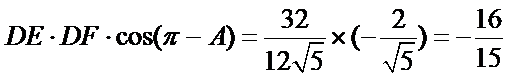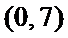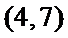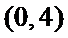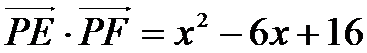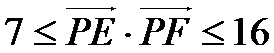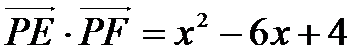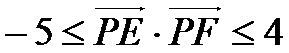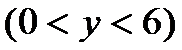- 平面向量数量积的运算
- 共301题
9.设




正确答案
解析
1.先画出可行域,将




考查方向
解题思路
1.先画出可行域,
2.将




易错点
1.无法将
2.可行域画错,导致结果出错。
知识点
16.已知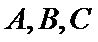
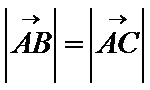
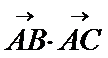
正确答案
解析
1.设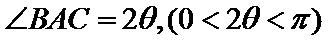
则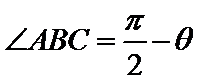
则
所以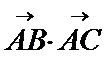
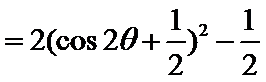
所以当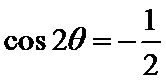
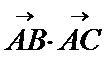
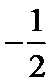
考查方向
易错点
1.不能正确引入变量表示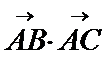
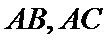
知识点
13.已知


正确答案
2
解析
由已知,
因为
所以
解得
应填2.
考查方向
解题思路
本题主要考查平面向量的坐标运算,向量的垂直等知识。
解题步骤如下:
①由向量垂直的条件,列出方程;
②解出方程,即得答案。
易错点
本题易把向量的平行和垂直的条件混淆,从而出现错误。
知识点
3.已知平面向量








正确答案
解析




考查方向
解题思路
先计算


易错点
忽略了

知识点
14.在锐角三角形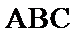

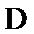
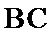
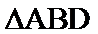
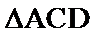
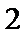
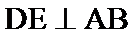
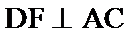
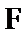
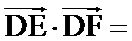
正确答案
解析
由题意得: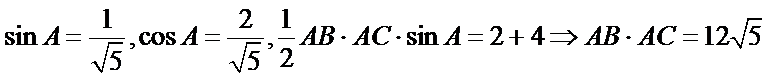
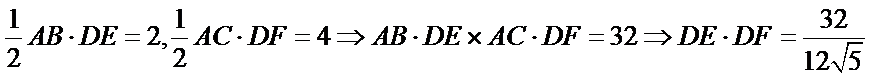
知识点
3.已知向量a,b满足a·(a-b)=2,且|a|=1,|b|=2,则a与b的夹角为
正确答案
解析
由



考查方向
解题思路
由已知先求

易错点
向量的夹角的余弦公式不清楚。
知识点
6. 若



正确答案
解析
由题可知:等比数列的相邻两项相乘仍然是等比数列。
A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
解题思路
代入特值计算或由等比数列的基本性质,即可得到结果。
A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在代特值时发生错误。
知识点
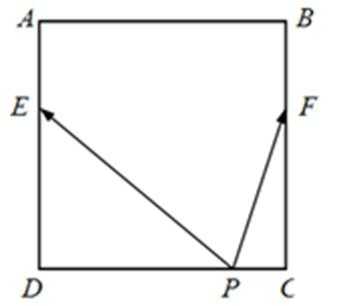
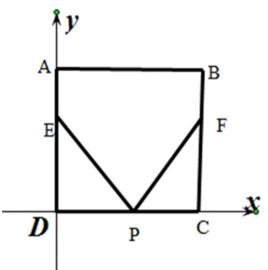
10.如图,正方形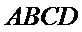
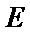
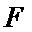
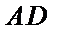
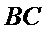
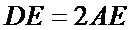
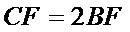
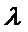
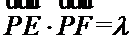
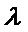
正确答案
解析
如图,
建立直角坐标系,则E(0,4)F(6,4)
(1)当P点在CD上时,设P(x,0)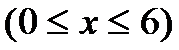
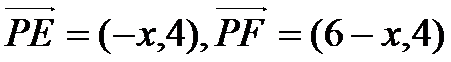
因为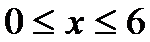
所以当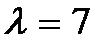
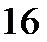
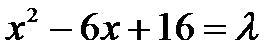
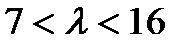
(2)当P点在AB上时,设P(x,6) 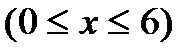
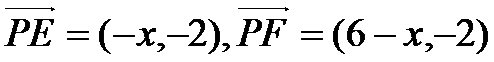
因为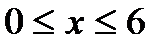
所以当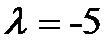
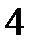
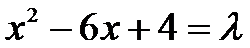
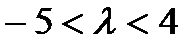
(3)当P点在AD上时(当P点在BC上的情况与在AD上相同),设P(0,y)
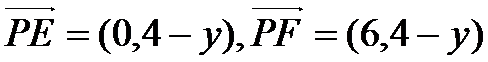
因为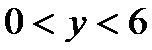
所以当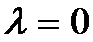
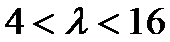
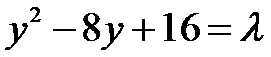
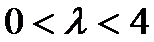
综上,当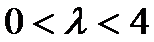
考查方向
解题思路
以D点为坐标原点建立直角坐标系,再分别讨论P点在AB,CD,以及AD和BC上的时候的情况,计算向量的数量积,并判断方程根的个数。(P在AD和BC上情况是一样的,不必分开讨论)
易错点
不能很好的判断方程根的个数
知识点
7.如图,菱形





正确答案
解析
以点A坐标为原点建立如图所示的直角坐标系,因为菱形的边长为2,可以得到A(0,0),B(2,0),C



考查方向
解题思路
建立适当的坐标系,利用线性规划理论,求目标函数最大值
易错点
没能正确建立坐标系
知识点
15.如图,菱形ABCD的边长为1,∠ABC=60°,E、F分别
为AD、CD的中点,则
正确答案
解析
考查方向
解题思路
本题考查了平面向量的数量积运算,可采用基向量法也可采用坐标法.基向量法需要选择合适的基底,
由于已知菱形的边长且


另外还可以尝试以

易错点
本题考查用基底表示时易错。
知识点
扫码查看完整答案与解析