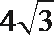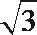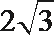- 平面向量数量积的运算
- 共301题
8. 已知



正确答案
解析
由余弦定理
则
又因为

即
即
由正弦定理得
即
所以,
考查方向
解题思路
先切化弦、化简向量的数量积,然后根据余弦定理、正弦定理进行化简即可得到答案。
易错点
不懂切化弦导致不知道从什么地方入手,对向量数量积不熟悉导致出错,在余弦定理的反应用时,不清楚余弦定理反过来也会化简。再者就是计算出错。
知识点
14.设四边形ABCD为平行四边形,


正确答案
9
解析
∵



∴









∴








故答案为:9.
考查方向
解题思路
1、由题可得

易错点
本题不容易想到用

知识点
3.已知向量



正确答案
解析
由


考查方向
本题主要考查了向量的垂直与模——向量的数量积运算,在近几年的各省高考题出现的频率较高,常单独命题或与解三角形、三角函数等知识点结合。
易错点
本题易在数量积运算上出错。
知识点
向量






正确答案
解析
由已知,得对




考查方向
本题主要考查了向量模的概念以及数量积的运算能力,也是常考题型
易错点
向量模的运算以及数量积的运算能力
知识点
已知角







正确答案
解:(1)由

且

∴

∴
(2)由余弦定理得
,而∵
由


当且仅当
又


所以

解析
本题属于三角函数的基本问题,题目的难度是中等,本题的关键是:
(1)、向量的基本运算以及三角函数恒等变换的应用;
(2)、余弦定理与基本不等式之间的应用,一直是考试的热点问题,
考查方向
本题考查了向量运算、三角函数恒等变换、正弦定理和余弦定理的综合应用
易错点
向量的运算、余弦定理的应用,需要注意
知识点
10.已知







正确答案
解析
由题可知,
考查方向
本题主要考查三角形的外接圆及向量的知识
解题思路
1、以AB,AC为基底表示AM,AO;
2、代入计算,即可得到结果。
A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在表示向量时发生错误。
知识点
3.平面向量
正确答案
解析




考查方向
本题主要考查两个向量的数量积的定义,求向量的模的方法,属于中档题
解题思路
先求出
易错点
数量积表示两个向量的夹角,向量的模
知识点
8.在
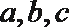
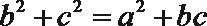
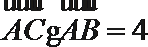

正确答案
解析
先求出A的余弦值,然后求出BC的值,然后求出A的正弦值,即可求出三角形的面积,所以选D
考查方向
本题主要考查余弦定理的应用,向量的数量积,考查计算能力
解题思路
利用余弦定理和正弦定理的交叉转换解题
易错点
概念混淆,计算能力差。
知识点
12.已知向量



正确答案
解析
考查方向
解题思路
本题主要是突破点在于垂直与数量积之间的转换
易错点
本题注意向量垂直与数量积之间的转换
知识点
15.设




正确答案
解析
由题可知,


考查方向
本题主要考查线性规划及向量的数量积。
解题思路
本题考查线性规划及向量的数量积,解题步骤如下:
1、画出平面区域。
2、化简数量积公式求解.
易错点
本题必须注意利用图像完成。
知识点
扫码查看完整答案与解析