平面向量数量积的运算
共301题

· 平面向量数量积的运算

平面向量数量积的运算
共301题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

11．对∈R，n∈[0，2]，向量c＝（2n＋3cosα，n－3sinα）的长度不超过6的概率为

正确答案

解析

考查方向

本题考察了向量的模长的几何意义，圆与圆的位置关系及其判定，考察了几何概型

解题思路

1)由向量可知，

2)向量转化问题变为圆的方程

长度不超过6等价于

3)问题转化为两圆内切或内涵，进而求出n的范围

4)根据几何概型得出结果

易错点

主要易错于几何意义的构建

知识点

平面向量数量积的运算与长度、角度有关的几何概型

题型：填空题

填空题 · 5 分

14.已知平面向量满足，且的夹角为120°，则的模的取值范围为 ▲ .

正确答案

解析

考查方向

本题主要考察了向量的减法及其几何意义，考察了向量的三角形法则，考察了正弦定理，该题比较综合，属于中档题

解题思路

1）根据题意使用有向线段表示向量，并构造三角形

2）利用三角形的正弦定理得出的模与夹角的关系，

3）根据角的取值范围得到取值范围

易错点

本题易错在无法找到有效的解题思路

知识点

平面向量数量积的运算数量积表示两个向量的夹角

题型：填空题

填空题 · 5 分

13.已知向量的夹角为，，若，则____.

正确答案

解析

由已知得,由于，所以,解得

考查方向

本题主要考查了平面向量的垂直、数量积问题，考查考生的运算能力。

解题思路

要求的值，需借助这个条件，而已知向量的模长及夹角，所以必须用来表示，从而求得的值。

易错点

不能理解什么样的向量可作基底。

知识点

平面向量数量积的运算数量积表示两个向量的夹角

题型：填空题

填空题 · 5 分

13.在中，点D满足，点是线段上的一个动点（不含端点），

若，则=______.

正确答案

解析

因为E在BD上

∴

考查方向

本题考查了平面向量的基本定理，三点共线原理的应用，属于基础题

解题思路

1、建立基底，所有的向量使用基底表示，2、使用共线条件得出关系

易错点

主要易错于三点共线的转换

知识点

向量的几何表示平面向量数量积的运算

题型：简答题

简答题 · 13 分

已知复数，为虚数单位，.

20.若为实数，求的值；

21.若复数对应的向量分别是，存在使等式成立，求实数的取值范围.

第(1)小题正确答案及相关解析

正确答案

（1）-2，

解析

：因为为实数

所以

因为，所以，

考查方向

本题主要考查复数的运算，三角函数的化简与求值，向量的坐标运算等知识，意在考查考生运算求解能力和转化能力。

解题思路

先根据复数的运算求出角；

易错点

不会利用求的值；

第(2)小题正确答案及相关解析

正确答案

（2）

解析

（2）由已知

因为

所以，

因为，所以，

进而，

解得 .

考查方向

本题主要考查复数的运算，三角函数的化简与求值，向量的坐标运算等知识，意在考查考生运算求解能力和转化能力。

解题思路

先根据向量的知识确定出函数关系

利用第（1）问的结论求函数的取值范围。

易错点

不会构建关于的函数，导致没有思路。

题型：单选题

单选题 · 5 分

11．（）

正确答案

解析

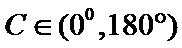
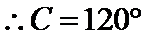
又。选D

考查方向

本题主要考查向量的数量积的运算和已知三角函数值求角等知识，意在考查考生的运算求解能力和转化与化归的能力。

解题思路

1。先根据题中给出的向量的数量积求出，

2.利用已知三角函数值求出角C的大小。

易错点

1.对于向量的知识掌握不好，以为向量和数量一样出错；

2.对于特殊角的三角函数值记忆出错。

知识点

平面向量数量积的运算

题型：单选题

单选题 · 5 分

9. 如图，菱形的边长为2，,为的中点，若为菱形内任意一点（含边界），则的最大值为( )

正确答案

解析

由平面向量的数量积的几何意义知，等于与在方向上的投影之积,所以

考查方向

本题主要考查平面向量的数量积和向量的线性运算等知识，意在考查考生的转化与化归和运算求解能力.

解题思路

1.先将所求的函数的最大值的情况找到；2.利用平面向量基本定理将，后带入题中给出的数据计算即可。

易错点

1.不知道最大是什么情况；2.不会将所求的向量用已知的向量去表示。

知识点

向量的几何表示平面向量数量积的运算

题型：填空题

填空题 · 5 分

15．已知两个非零平面向量满足：对任意恒有，若，则 .

正确答案

考查方向

本题考查平面向量的数量积以及模的运算。

解题思路

原不等式可以转化为关于的一元二次方程，再转成二次不等式恒成立问题。

易错点

不明确不等式的转型

知识点

平面向量数量积的运算平面向量的综合题

题型：单选题

单选题 · 5 分

3.已知平面向量，，，满足，，且，则下列结论一定成立的是

正确答案

解析

，两边同时乘以,,因为>0,所以x>0, 两边同时乘以,,因为>0,所以y<0,

考查方向

向量的数量积运算

解题思路

可以由已知条件, ,两边分别乘以a,b向量, 再利用题中的条件, 求解。

易错点

数量积的运算律易出错

知识点

平面向量数量积的运算

题型：填空题

填空题 · 4 分

15.已知点是线段上一点，，，则的最小值为 ▲ ．

正确答案

解析

设向量=, =β,=γ,已知=得 =,所以

所以|MA|:|MB|=|AC|:|CB|=2：1=k,==,

当=-1时，取得最小值，最小值为

考查方向

本题考查平面向量的数量积的综合应用

解题思路

先化简已知条件= ，得出向量=，MC为角MAB内角平分线， |MA|:|MB|=|AC|:|CB|=K，将所求代数式中的MA,MA,AB, 用K来表示, 通过向量MA与MB的夹角求出代数式的最小值

易错点

本题在由平面向量数量关系，转化到平面几何图形的相关数据

知识点

平面向量数量积的运算

继续学习学习下一知识点

下一知识点 : 数量积表示两个向量的夹角

百度题库 > 高考 > 理科数学 > 平面向量数量积的运算

扫码查看完整答案与解析