- 平面向量数量积的运算
- 共301题
15.在正方形





正确答案
[4,8-2
解析
设CN=x,CM=y,

因为

















考查方向
解题思路
画出正方形,设CN=x,CM=y,将
易错点
处理变量之间的整体关系及转化
知识点
13.已知





正确答案
解析
如图所示,点M 在△ABC 内部(不含边界)
则
此时n=0,又M不在边界上,所以n>0
过D 点作平行于 AC 的直线,并交BC 于F 点,则
此时, 
综上, n 的取值范围为
考查方向
解题思路
由题根据

易错点
本题在根据平行四边形法则由
知识点







正确答案
考查方向
解题思路
1. 运用B,C,P共线,则
易错点
不能利用m与n的关系建立动点横坐标x与纵坐标y之间的联系。
知识点
已知平面向量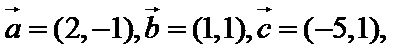
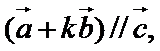
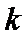
正确答案
解析
由

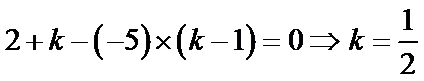
考查方向
解题思路
由
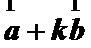
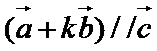

易错点
本题易在坐标运算上出错。
知识点
已知向量

17.若

18.在




正确答案
解析

得
即


考查方向
解题思路
先通过向量垂直,得到三角关系,利用辅助角公式得到三角函数的解析式y=sin(x-



易错点
向量的坐标运算,三角函数的恒等变换
正确答案
(0,
解析
由

∴







考查方向
解题思路
将边用正弦定理进行转化,得到cosA=


易错点
向量的坐标运算,三角函数的恒等变换
8.已知菱形





正确答案
解析
如图,因为




考查方向
解题思路
画出图形,分别把

易错点
不会利用向量加法的几何意义运算或进行向量的数量积运算时,夹角出错,
知识点
7.已知菱形





正确答案
解析





考查方向
解题思路
画出图形,分别把

易错点
不会利用向量加法的几何意义运算或进行向量的数量积运算时,夹角出错,
知识点
已知
17.若







正确答案
解析
(Ⅰ)



考查方向
解题思路
化简


易错点
通过降幂公式、辅助角公式化简

正确答案

解析









考查方向
解题思路
化简


易错点
通过降幂公式、辅助角公式化简

关于打击与保护,下列哪些说法正确( )
A.打击与保护是对立的
B.公安工作具有打击与保护的双重特点
C.打击中包含着警戒预防,使人不敢以身试法
D.保护中包含着消除造成违法犯罪的消极因素
正确答案
B,C,D
解析
[解析] 公安工作具有打击与保护的双重特点,这是由公安工作的对象所决定的。打击与保护,两者是紧密联系、相互依存、相互渗透、互为前提的。打击中包含着警戒预防,使人不敢以身试法;保护中包含着消除造成违法犯罪的消极因素。故选BCD。
为了迎接2010年广州亚运会,某大楼安装5个彩灯,它们闪亮的顺序不固定。每个彩灯闪亮只能是红、橙、黄、绿、蓝中的一种颜色,且这5个彩灯闪亮的颜色各不相同,记这5个彩灯有序地闪亮一次为一个闪烁。在每个闪烁中,每秒钟有且只有一个彩灯闪亮,而相邻两个闪烁的时间间隔均为5秒。如果要实现所有不同的闪烁,那么需要的时间至少是
正确答案
解析
共有5!=120个不同的闪烁,每个闪烁时间为5秒,共5×120=600秒;每两个闪烁之间的间隔为5秒,共5×(120-1)=595秒。那么需要的时间至少是600+595=1195秒。
知识点
扫码查看完整答案与解析