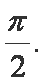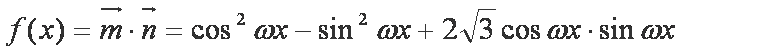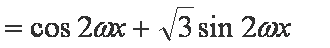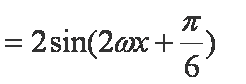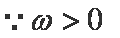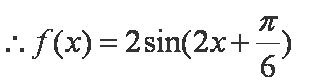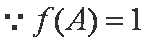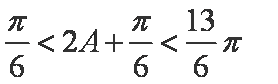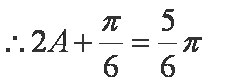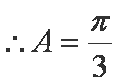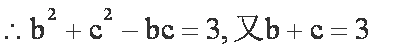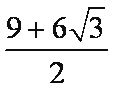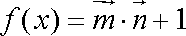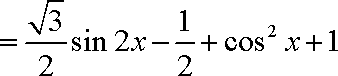- 平面向量数量积的运算
- 共301题
1
题型:简答题
|
已知椭圆






(1)求椭圆
(2)过椭圆左焦点





正确答案
见解析。
解析
(1)



∴椭圆E的方程为:
(2)设点

由方程组


由已知得:
知识点
平面向量数量积的运算向量在几何中的应用椭圆的定义及标准方程直线、圆及圆锥曲线的交汇问题
1
题型:简答题
|
已知函数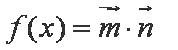
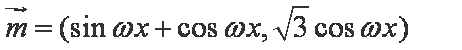
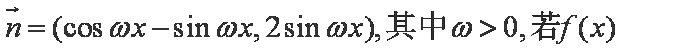
(1)求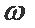
(2)在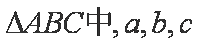
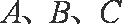
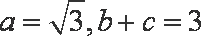
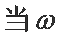
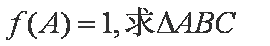
正确答案
见解析
解析
解析:(1)
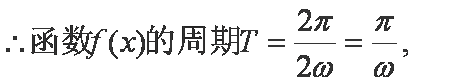
解得
(2)由(1)可知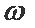

由余弦定理知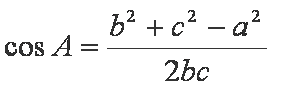
联立解得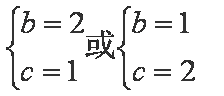
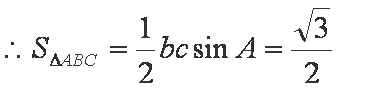
知识点
三角函数中的恒等变换应用正弦定理余弦定理平面向量数量积的运算
1
题型:填空题
|
已知等边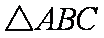


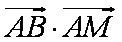
正确答案
解析
略
知识点
平面向量数量积的运算向量在几何中的应用
1
题型:简答题
|
已ΔABC的内角A,B,C对的边分别为 a,b,c 



(1)求角A的大小;
(2)若a = 1,求b +c的取值范围.
正确答案
(1)
解析
(1)由


再由正弦定理得:
又
所以
又
(2)由正弦定理得


故b+c的取值范围为(1,2] . ……12分
知识点
正弦定理余弦定理平面向量数量积的运算量积判断两个平面向量的垂直关系
1
题型:简答题
|
已知向量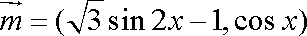
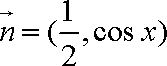
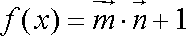
(1)求函数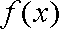
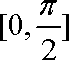
(2)已知在
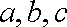
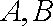
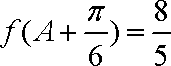
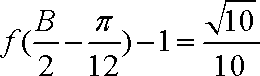
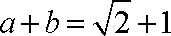
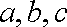
正确答案
见解析
解析
(1)函数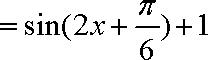
∴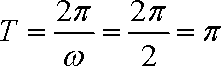
∵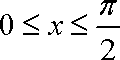
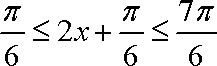
∴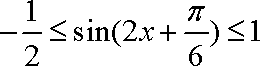
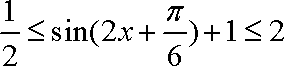
∴函数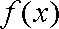
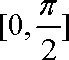
(2)∵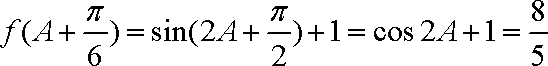
∴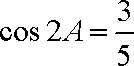
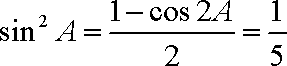
∵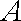
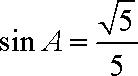
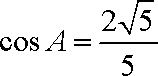
又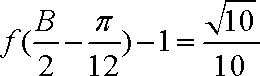
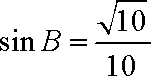
∵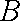
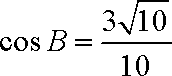
由正弦定理得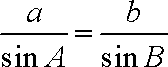
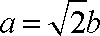
又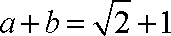
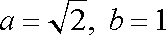
而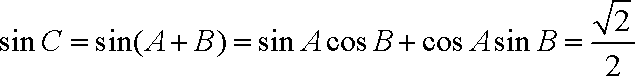
由正弦定理得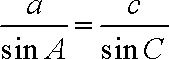
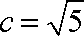
知识点
三角函数的周期性及其求法三角函数中的恒等变换应用解三角形的实际应用三角函数的最值平面向量数量积的运算
下一知识点 : 数量积表示两个向量的夹角
扫码查看完整答案与解析