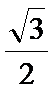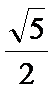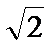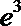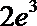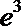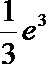- 曲线与方程
- 共215题
14.由直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.由曲线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.点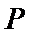
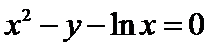
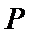
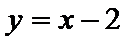
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知点




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设曲线y=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若曲线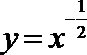
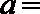
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.曲线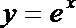
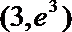
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22、23、24三题中任选一题作答。注意:只能做所选定题目。如果多做,则按所做的第一个题目计分。
22.如图,在正△ABC中,点D,E分别在边AC, AB上,且AD=

(Ⅰ)求证:a,e,f,d四点共圆;
(Ⅱ)若正△ABC的边长为2,求A,E,F,D所在圆的半径.
23. 设
(Ⅰ)当

(Ⅱ)当



24. 已知曲线





(Ⅰ)写出直线

(Ⅱ)设曲线






正确答案
22.(Ⅰ)证明:∵AE=

∵在正△ABC中,AD=
又∵AB=BC,∠BAD=∠CBE,
∴△BAD≌△CBE, ∴∠ADB=∠BEC,
即∠ADF+∠AEF=π,所以A,E,F,D四点共圆.
(Ⅱ)解:如图, 取AE的中点G,连接GD,则AG=GE=
∵AE=


∵AD=

∴GD=AG=AD=

所以点G是△AED外接圆的圆心,且圆G的半径为
由于A,E,F,D四点共圆,即A,E,F,D四点共圆G,其半径为
23. (I)


所以解集为
(II)当


由图像知:当



所以实数

24.(Ⅰ)
(II)


所以当



解析
解析已在路上飞奔,马上就到!
知识点
9.曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析