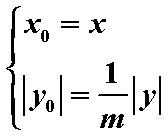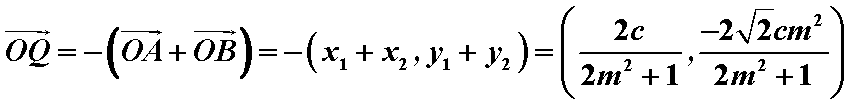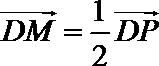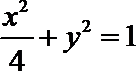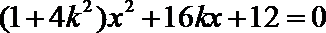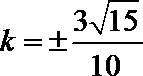- 曲线与方程
- 共215题
已知函数

(1)当


(2)求
正确答案
见解析
解析
(1)解:当


由于

所以曲线


(2)解:

① 当






当



② 当





③ 当

④ 当





知识点
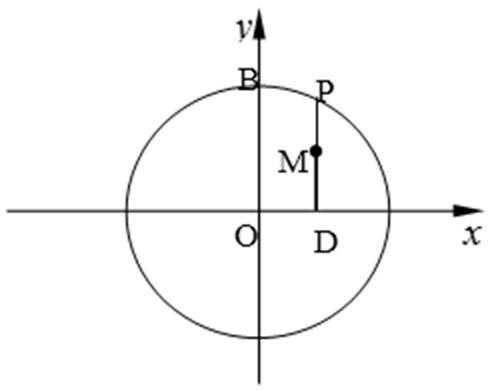
设P是圆x2+y2=4上的任意一点,过P作x轴的垂线段PD,D为垂足, M是线段PD上的点,且满足|DM|=m|PD|(0<m<1),当点P在圆上运动时,记M的轨迹为曲线C.
(1)求曲线C的方程;
(2)过曲线C的左焦点F作斜率为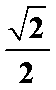
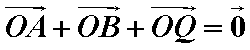
正确答案
见解析
解析
(1)如图设M(x,y)、P(x0,y0),则由|DM|=m|PD|(0<m<1)得
x= x0,|y|=m| y0|,即
∵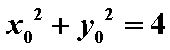
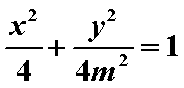
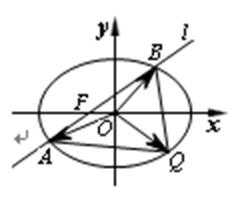
(2)设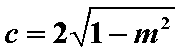
由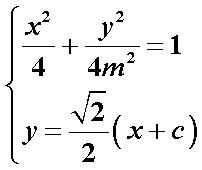
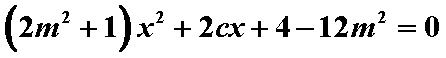
设A(x1,y1)、B(x2,y2).
则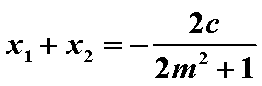
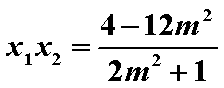
∴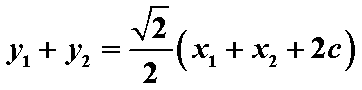
∵
即Q点坐标为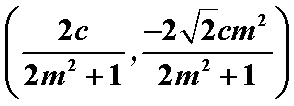
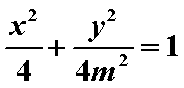
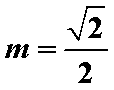
∴存在当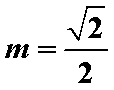
知识点
若双曲线



正确答案
解析
由题可知




知识点
设函数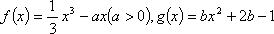
(1)若曲线

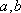
(2)当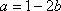
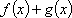
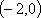

(3)当

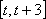
正确答案
见解析
解析
(1)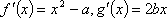
因为曲线
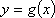
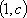
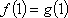
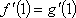
即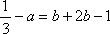
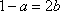
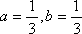
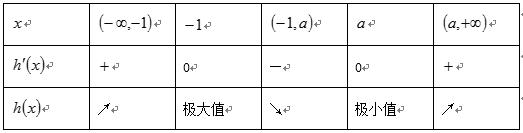
(2)记
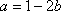
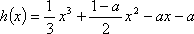
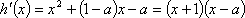
令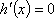
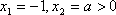
当
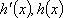
所以函数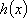
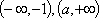
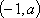
故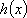
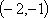
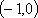
从而函数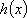
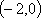
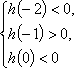
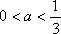

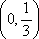
(3)记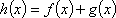

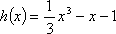
由(2)可知,函数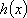
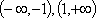
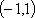
①当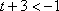
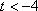
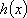
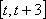
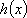

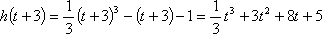
②当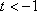
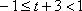
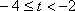



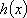
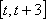
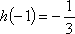
当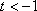
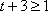
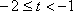
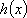

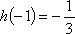
③当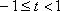
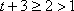
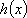
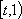
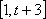
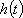
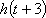
由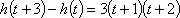
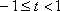
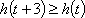
所以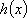
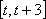
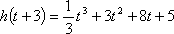
④当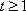
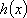
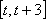
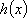
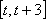
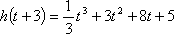
知识点
设椭圆

(1)求椭圆的方程;
(2)求动点C的轨迹E的方程;
(3)设直线AC(C点不同于A,B)与直线x=2交于点R,D为线段RB的中点,试判断直线CD与曲线E的位置关系,并证明你的结论。
正确答案
见解析。
解析
知识点
设椭圆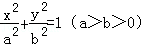
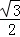
(1)求椭圆的方程;
(2)求动点C的轨迹E的方程;
(3)设直线AC(C点不同于A,B)与直线x=2交于点R,D为线段RB的中点,试判断直线CD与曲线E的位置关系,并证明你的结论。
正确答案
见解析。
解析
解:(1)由题意,可得a=2,e=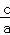
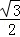
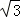
因此,椭圆的方程为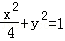
(2)设C(x,y),P(x0,y0),由题意得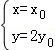
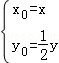
又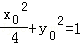
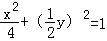
即动点C的轨迹E的方程为x2+y2=4。
(3)设C(m,n),点R的坐标为(2,t),
∵A、C、R三点共线,∴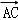
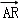
而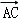
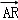
∴t=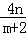
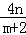
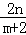
∴直线CD的斜率为k=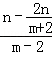

而m2+n2=4,∴﹣n2=m2﹣4,代入上式可得k=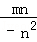
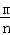
∴直线CD的方程为y﹣n=﹣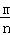
∴圆心O到直线CD的距离d=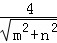
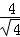
因此,直线CD与圆O相切,即CD与曲线E相切。
知识点
已知





(1)求点P的轨迹方程;
(2)是否存在定直线

正确答案
(1)y2=x(2)x=
解析
(1)设B(0,t),设Q(m,0),t2=







2










(2)由(1),点P的轨迹方程是y2=x;设P(y2,y),


L=2
=2

若a为常数,则对于任意实数y,L为定值的条件是a-





知识点
已知







正确答案
解析
第一步识别条件:椭圆





第二步转化条件: 应该想到在向量一章里面学过这个重心的坐标表示可以用三个顶点表示啊 G((x1+x2+x3)/3,(y1+y2+y3)/3),再看看图形,发现太好了, 三个点中,F1,F2关于原点是对称的,x1+x2=0,y1+y2=0这下可好了。
第三步看问定向:重心
第四步结论已出现:
知识点
已知椭圆





(1)求该椭圆的标准方程;
(2)当点













正确答案
见解析
解析
(1)由










故椭圆的标准方程为 
(2)设

则


动点


由
设



因为点


故
所以







知识点
21.如图,圆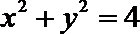

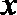
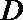
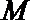
(1)求动点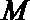
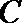
(2)过点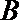

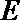
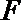

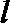
正确答案
(1)设
则由题意得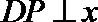
所以
又P在圆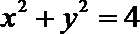
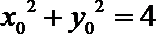
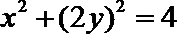
轨迹是以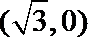
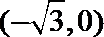
长轴长为4的椭圆。
(2)方法一:当直线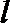
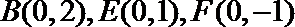
设直线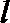
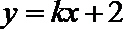
代入椭圆方程得:
△
设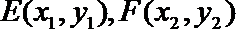
则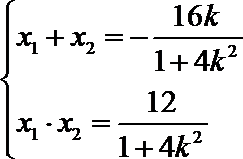
由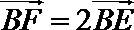
所以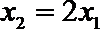
由(*)、(**)
解得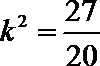
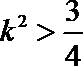
所以
即所求直线方程为: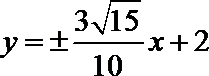
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析