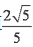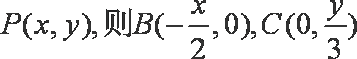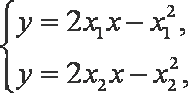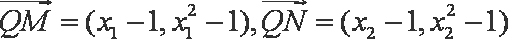- 曲线与方程
- 共215题
如图,已知点S(-2,0)和圆

(1)求
(2)设n是过原点的直线,




正确答案
见解析
解析
(1)易得




直线PS与TE交于C,故


①②相乘得

要使


即

(2)设A,B两点的坐标分别为


(ⅰ)当


由




∵

即

由求根公式可得


=
将④,⑤代入上式并化简得 
将



(ⅱ)当


当X=1时,A,B,Q的坐标分别为

∴



综上可知,使

·
知识点




(1)若曲线C1关于曲线C2对称,求“的值,并把曲线C1和C2化成直角坐标方程;
(2)求|OA|·|OC|+|OB|·
正确答案
见解析
解析
解:(1)








(2)


知识点
已知函数

(1)若曲线




(2)当




(3)若




正确答案
见解析。
解析
(1)

∵曲线


∴ 

(2)设

又在点
∴

设

∴



从而,结合(1)可知,满足题设的点

(3)当



曲线



由

∵ 曲线



即

若




从而,方程

令

∴ 当









所以,要使方程


知识点
已知










(1)求曲线
(2)设曲线




(3)在(1)、(2)的条件下,直线




点



正确答案
(1)

解析
(1)设动圆圆心的坐标为
因为动圆在







(2)依题意,







(3)设直线





将
两式相减得





由(2)知

由题设

即
知识点
已知O为坐标原点,向量

正确答案
解析
略
知识点
如图,在圆







(1)当点



(2)若圆





正确答案
见解析
解析
(1)设





即点


(2)解法一:
(i) 当直线




(ii)当直线


因为直线



又直线



所以直线


由




综上(i)(ii)知,直线

解法二 :设


(i)当





(ii)当



令



所以直线


由





综上(i)(ii)知,直线

知识点
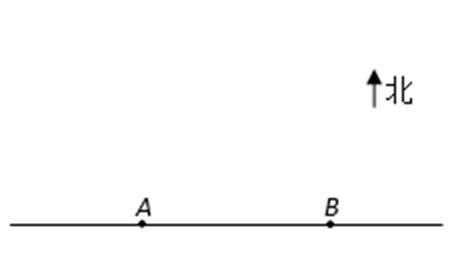
为了监测某海域的船舶航行情况,海事部门在该海域设立了如图所示东西走向,相距


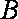
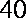
(1)建立适当的平面直角坐标系,求观测区域边界曲线的方程;
(2)某日上午7时,观测站B发现在其正东10海里的C处,有一艘轮船正以每小时8海里的速度向北偏西45°方向航行,问该轮船大约在什么时间离开观测区域?
(参考数据:
正确答案
见解析
解析
本题主要考查直线、椭圆、直线与椭圆的位置关系等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、化归与转化思想,考查应用意识。
以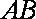
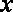
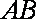
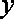
(1)依题意可知:考察区域边界曲线是以A,B为焦点的椭圆,…………2分
设椭圆方程为: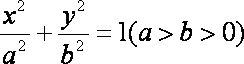
则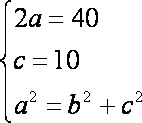
解得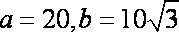
∴考察区域边界曲线的方程为: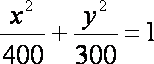
(2)设轮船在观测区域内航行的时间为
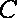

∵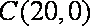

∴直线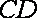
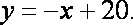
联立方程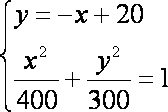
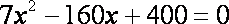
解得
∴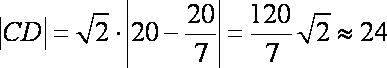
∴ 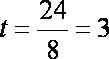
∴轮船大约在当日上午10时离开观测区域. . ……………………………13分
(其他解法相应给分)
知识点
已知点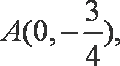
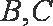
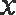
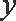

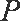
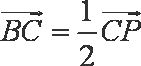
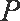
(1)求曲线E的方程;
(2)点Q(1,a),M,N为曲线E上不同的三点,且

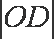
正确答案
(1)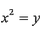
解析
解析:(1)解:设



(2)解法一:易知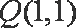
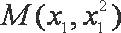
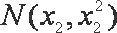
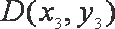
设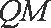
联立方程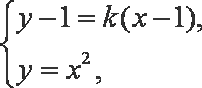
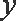
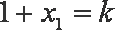
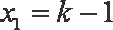
同理,设

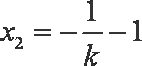
对函数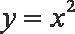
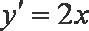
所以抛物线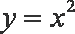


所以切线
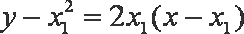
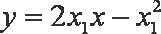
同理,抛物线


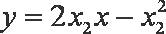
联立两条切线的方程
解得

所以点


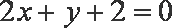
因为点
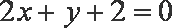

所以

由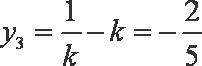
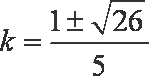
所以当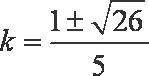
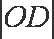
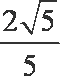
解法二:由题意,

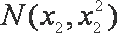

对函数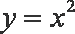
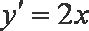
所以抛物线
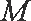
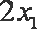
所以切线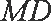

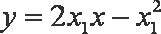
同理,抛物线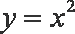


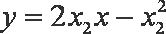
联立两条切线的方程
解得
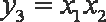
又
由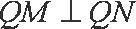
所以点

因为点
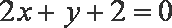
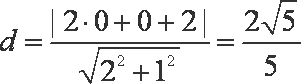
所以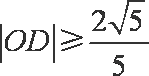
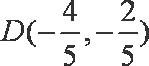
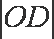
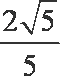
知识点
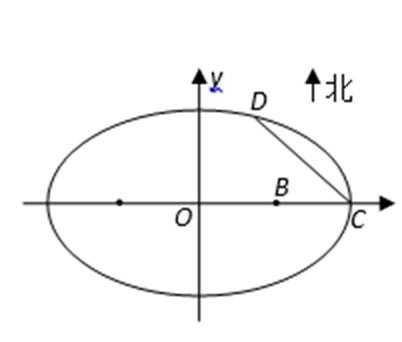
在平面直角坐标系中,曲线C1的参数方程为 





(1)求曲线C1,C2的方程;
(2)A(ρ1,θ),Β(ρ2,θ+

正确答案
见解析
解析
解析:(1)将M




所以

设圆C2的半径R,则圆C2的方程为:ρ=2Rcosθ(或(x-R)2+y2=R2),将点D
∴R=1 ∴圆C2的方程为:ρ=2cosθ(或(x-1)2+y2=1)--------5分
(2)曲线C1的极坐标方程为:


所以
即

知识点
已知曲线





(1)写出直线

(2)设曲线






正确答案
见解析
解析
解析:(1)

(2)



所以当



知识点
扫码查看完整答案与解析