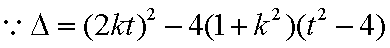- 曲线与方程
- 共215题
已知平面内的一个动点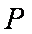


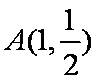
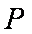

(1)求曲线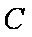
(2)过原点
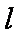


正确答案
见解析
解析
(1)设动点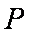

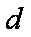
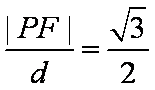
∵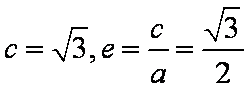
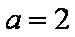
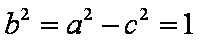
故椭圆

(2)若直线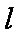
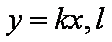
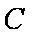

将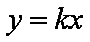
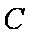
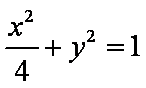
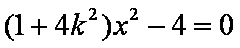
∴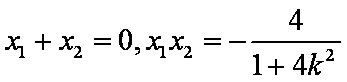
∴
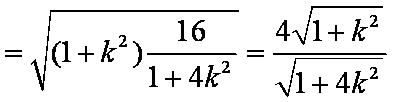
又点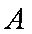
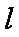
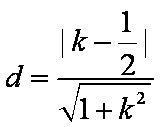
∴
① 当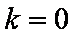
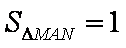


③当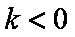

若直线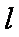
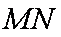

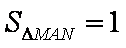
综上,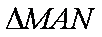
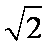
知识点
选修4-4:坐标系与参数方程
在极坐标系中,过点

(1)将

(2)在极坐标系中,以极点为坐标原点,以极轴为
若曲线






正确答案
见解析。
解析
(1)画图可知
(2)直线



知识点
在直角坐标平面内,将每个点绕原点按逆时针方向旋转





(1)求矩阵

(2)求曲线


正确答案
(1)
解析
(1)在直角坐标平面内,将每个点绕原点按逆时针方向旋转


(2)将每个点横、纵坐标分别变为原来的







(1)


(2)




故所求的曲线方程为:
知识点
在直角坐标平面内,以坐标原点






(1)分别求出曲线

(2)若点




正确答案
(1)

解析
(1)由曲线






(2)由圆心(2,0)到直线




(1)由







即
(2)因为圆心







知识点
若以曲线y=f(x)任意一点M(x,y)为切点作切线l,曲线上总存在异于M的点N(x1 y1),以点N为切点作切线l1,且l∥l1,则称曲线y=f(x)具有“可平行性”,下列曲线具有可平行性的编号为 ,(写出所有满足条件的函数的编号)
①y=x3﹣x
②y=x+
③y=sina
④y=(x﹣2)2+lnx。
正确答案
②③
解析
由题意得,曲线具有可平行性的条件是:方程y′=a(a是导数值)至少有两个根,
①、由y′=3x2﹣1知,当y′=﹣1时,x的取值唯一,只有0,不符合题意;
②、由y′=1﹣

③、由y'=cosx和三角函数的周期性知,cosx=a(﹣1≤a≤1)的解有无穷多个,符合题意;
④、由y'=2x﹣4+

知识点
选修4-4:坐标系与参数方程
已知曲线C1:


(1)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(2)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线




正确答案
见解析。
解析
(1)







因为圆心


所以

(2)压缩后的参数方程分别为





化为普通方程为:



联立消元得
其判别式
所以压缩后的直线



知识点
选修4—2:矩阵与变换
设矩阵
(1)若

(2)若曲线C:


求
正确答案
见解析。
解析
(1)当

(2)设曲线C上任意一点


又点



即
又已知曲线C的方程为
比较系数可得


知识点
已知圆C1的方程为

(1)求动圆圆心C的轨迹M的方程;
(2)斜率为k的直线l与轨迹M相切于第一象限的点P,过点P作直线l的垂线恰好经过点A(0,6),并交轨迹M于异于点P的点Q,记

正确答案
见解析
解析
解(1)设动圆圆心C的坐标为

可得 
由于圆C1在直线l的上方,所以动圆C的圆心C应该在直线l的上方,所以有


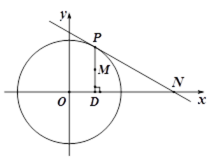
(2)如图示,设点P的坐标为







把直线PQ的方程与轨迹M的方程联立得



知识点
选修4-2:矩阵与变换
若点




(2)求曲线C:x2+y2=1在矩阵N=
正确答案
见解析。
解析
法一:



即M=




法二:同法一可求得M=






(2)
知识点
如图,在圆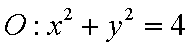
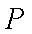
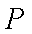
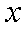
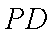
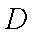
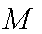
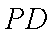
(1)当点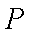

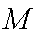
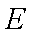
(2)若圆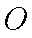
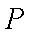
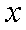
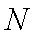


正确答案
(1)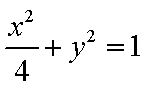
解析
(1)由于点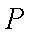

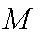
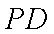
(2)由(1)得到轨迹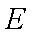


(1)设
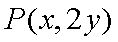

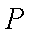


即点
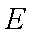

(2)解法一:
(i) 当直线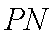


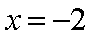
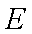
(2)当直线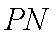

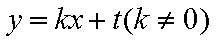
因为直线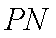

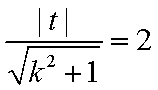
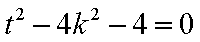
又直线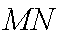
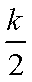
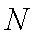
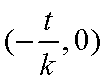
所以直线
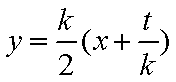
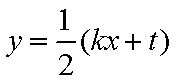
由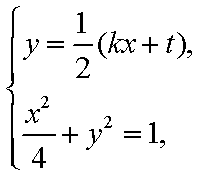
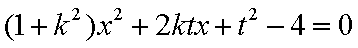
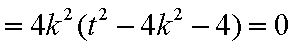

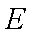
综上(i)(2)知,直线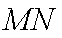
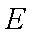
解法二 :设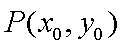

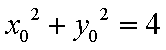
(i)当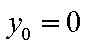


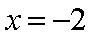


(2)当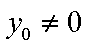

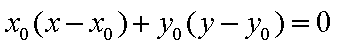
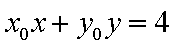
令
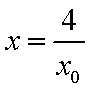
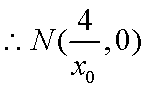
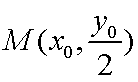
所以直线
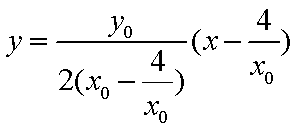

由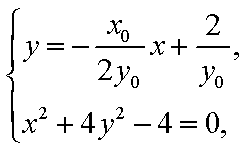

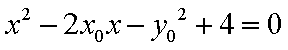
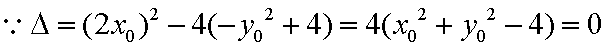
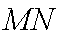

综上(i)(2)知,直线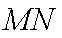

知识点
扫码查看完整答案与解析